The Spread of the Sapphire/Slammer Worm
The Spread of the Sapphire/Slammer Worm
By (in alphabetical order)
| David Moore | Vern Paxson | Stefan Savage | Colleen Shannon | Stuart Staniford | Nicholas Weaver |
| CAIDA & UCSD CSE |
ICIR & LBNL |
UCSD CSE | CAIDA | Silicon Defense | Silicon Defense & UC Berkeley EECS |
Introduction
The Sapphire Worm was the fastest computer worm in history. As it began spreading throughout the Internet, it doubled in size every 8.5 seconds. It infected more than 90 percent of vulnerable hosts within 10 minutes.
The worm (also called Slammer) began to infect hosts slightly before 05:30 UTC on Saturday, January 25. Sapphire exploited a buffer overflow vulnerability in computers on the Internet running Microsoft's SQL Server or MSDE 2000 (Microsoft SQL Server Desktop Engine). This weakness in an underlying indexing service was discovered in July 2002; Microsoft released a patch for the vulnerability before it was announced[1]. The worm infected at least 75,000 hosts, perhaps considerably more, and caused network outages and such unforeseen consequences as canceled airline flights, interference with elections, and ATM failures. Several disassembled versions of the source code of the worm are available. [2].
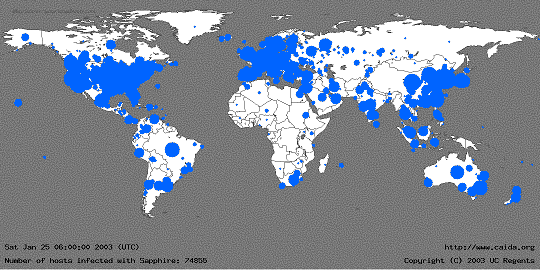
Figure 1: The
geographic spread of Sapphire in the 30 minutes after release. The
diameter of each circle is a function of the logarithm of the number
of infected machines, so large circles visually underrepresent the
number of infected cases in order to minimize overlap with adjacent
locations. For some machines, only the country of origin can be
determined (rather than a specific city).
Propagation speed was Sapphire's novel feature: in the first minute, the infected population doubled in size every 8.5 (±1) seconds. The worm achieved its full scanning rate (over 55 million scans per second) after approximately three minutes, after which the rate of growth slowed down somewhat because significant portions of the network did not have enough bandwidth to allow it to operate unhindered. Most vulnerable machines were infected within 10-minutes of the worm's release. Although worms with this rapid propagation had been predicted on theoretical grounds [5], the spread of Sapphire provides the first real incident demonstrating the capabilities of a high-speed worm. By comparison, it was two orders magnitude faster than the Code Red worm, which infected over 359,000 hosts on July 19th, 2001 [3]. In comparison, the Code Red worm population had a leisurely doubling time of about 37 minutes.
While Sapphire did not contain a malicious payload, it caused considerable harm simply by overloading networks and taking database servers out of operation. Many individual sites lost connectivity as their access bandwidth was saturated by local copies of the worm and there were several reports of Internet backbone disruption [4] (although most backbone providers appear to have remained stable throughout the epidemic). It is important to realize that if the worm had carried a malicious payload, had attacked a more widespread vulnerability, or had targeted a more popular service, the effects would likely have been far more severe.
This document is a preliminary analysis of the Sapphire worm, principally focused on determining the speed and scope of its spread and the mechanisms that were used to achieve this result.
Sapphire: A Random Scanning Worm
Sapphire's spreading strategy is based on random scanning -- it selects IP addresses at random to infect, eventually finding all susceptible hosts. Random scanning worms initially spread exponentially rapidly, but the rapid infection of new hosts becomes less effective as the worm spends more effort retrying addresses that are either already infected or immune. Thus as with the Code Red worm of 2001, the proportion of infected hosts follows a classic logistic form of initially exponential growth in a finite system [5,3]. We refer to this as the random constant spread (RCS) model.
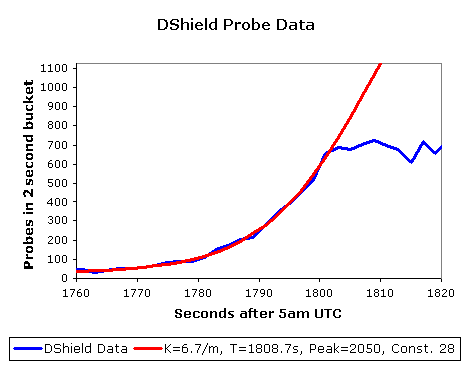
Sapphire's spread initially conformed to the RCS model, but in the later stages it began to saturate networks with its scans, and bandwidth consumption and network outages caused site-specific variations in the observed spread of the worm. A dataset from the DShield project [8] fit to a RCS model is shown below. The model fits extremely well up to a certain point when the probe rate abruptly levels out. This change in growth of the probe rate is due to the combined effects of bandwidth saturation and network failure (some networks shut down under the extreme load).
Based on analysis of a number of datasets, we estimate the initial compromise rate (the number of hosts that a worm instance can infect per second) was 7 (±1) per minute, equivalent to a global doubling time of 8.5 ±1 seconds.
Why Sapphire Was So Fast
Sapphire spread nearly two orders of magnitude faster than Code Red, yet it probably infected fewer machines. Both worms used the same basic strategy of scanning to find vulnerable machines and then transferring the exploitive payload; they differed in their scanning constraints. While Code Red was latency limited, Sapphire was bandwidth-limited, allowing it to scan as fast as the compromised computer could transmit packets or the network could deliver them.
Sapphire contains a simple, fast scanner in a small worm with a total size of only 376 bytes. With the requisite headers, the payload becomes a single 404-byte UDP packet. This can be contrasted with the 4kb size of Code Red, or the 60kb size of Nimda. Previous scanning worms, such as Code Red, spread via many threads, each invoking connect() to probe random addresses. Thus each thread's scanning rate was limited by network latency, the time required to transmit a TCP-SYN packet and wait for a response or timeout. In principal, worms can compensate for this latency by invoking a sufficiently large number of threads. However, in practice, context switch overhead is significant and there are insufficient resources to create enough threads to counteract the network delays -- the worm quickly stalls and becomes latency limited.
In contrast, Sapphire's scanner was limited by each compromised machine's bandwidth to the Internet. Since the SQL Server vulnerability was exploitable using a single packet to UDP port 1434, the worm was able to send these scans without requiring a response from the potential victim. The inner loop is very small, and since modern servers have sufficient network I/O capacity to transmit network data at 100Mbps+, Sapphire was frequently limited by the access bandwidth to the Internet rather than its own ability to generate new copies of itself. In principle, an infected machine with a 100 Mb/s connection to the Internet could produce over 30,000 scans/second. In practice, due to bandwidth limitations and the per-packet overhead, the largest probe rate we directly observed was 26,000 scans/second, with an Internet-wide average of approximately 4,000 scans/second per worm during the early phase of growth.
The Sapphire worm's scanning technique was so aggressive that it quickly interfered with its own growth. Consequently, the contribution to the rate of growth from later infections was diminished since these instances were forced to compete with existing infections for scarce bandwidth. Thus Sapphire achieved its maximum Internet-wide scanning rate within minutes.
Any future single packet UDP worm will probably have the same property unless its spread is deliberately limited by the author, as a simple loop will create a bandwidth-limited scanner. While a TCP-based worm, such as Code Red, could also employ a bandwidth-limited scanner by sending TCP-SYNs at maximum rate and responding automatically to any replies in another thread, this would require more effort to implement correctly.
Sapphire's Pseudo Random Number Generator
For a random-scanning worm to be effective, it needs a good source of "random" numbers to select new targets to attack. Sapphire's random number generator turned out to have some interesting deficiencies which both made our analysis difficult, and perhaps had implications for future worms.
Sapphire uses a linear congruent, or power residue, pseudo random number generation (PRNG) algorithm. These algorithms are of the form: x' = (x * a + b) mod m, where x' is the new pseudo-random number to be generated, x is the last pseudo-random number generated, m represents the range of the result, and both a and b are carefully chosen constants. Linear congruent generators can be implemented very efficiently and with proper values of a and b they have reasonably good distributional properties (although they are not random from a sequence standpoint). The initial value of the generator is typically "seeded" with a source of higher quality random numbers to ensure that the precise sequence is not identical between runs.
The writers of Sapphire intended to use a linear congruent parameterization popularized by Microsoft, x' = (x * 214013 + 2531011) mod 2^32. However, they made two mistakes in its implementation. First, they substituted their own value for the increment: the hex number 0xffd9613c. This value is equivalent to -2531012 when interpreted as a 2's complement decimal, so it seems likely that their representation was in error, and possibly they intended to use the SUB instruction to compensate, but mistakenly used ADD instead. The end result is that the increment is always even. Their second mistake was to misuse the OR instruction, instead of XOR, to clear a key register -- leaving the register's previous contents intact. As a result, the increment is accidentally XORed with the contents of a pointer contained in SqlSort's Import Address Table (IAT). Depending on the version of the SqlSort DLL this "salt" value will differ, although two common values, which we have directly observed, are 0x77f8313c and 0x77e89b18. EEye also reports seeing 0x77ea094c [2].
These mistakes significantly reduce the quality of the generator's distribution. Since b is even and the salt is always 32-bit aligned, the least-significant two bits are always zero. Interpreted as a big-endian IP address this ensures that the 25th and 26th bits in the scan address (the upper octet) will stay constant in any execution of the worm. Similar weaknesses extend to the 24th bit of the address depending on the value of the uncleared register. Moreover, with the incorrectly chosen increment, any particular worm instance will cycle through a list of addresses significantly smaller than the actual Internet address space. Thus there are many worm instances which will never probe our monitored addresses, because none of these addresses are contained in the cycle which the worm scans. This, combined with the size of our monitored address space [6], prevents us from directly measuring the number of infected hosts during the first minutes of the worm's spread.
It happens that Sapphire will include or not include entire /16 blocks of addresses in a cycle. We were able to assemble lists of the address blocks in each cycle for each value of the salt (the cycle structure is salt dependent).
Fortunately the probability of choosing a particular cycle is directly proportional to the size of the cycle if the initial seed is selected uniformly at random. When considered over many randomly seeded worms, all Internet addresses are equally likely to be probed. Thus we can accurately estimate the scanning rate of the worm during the progress of the infection by monitoring relatively small address ranges. Since the probing will cover all Internet addresses, we can also estimate the percentage of the Internet infected.
If not for the initial seed, these flaws would prevent the worm from reaching large portions of the Internet address space, no matter how many hosts were infected. For the same reason, these flaws could also bias our measurements, since even though our data comes from several different networks, there is a small chance that these particular networks were disproportionately more or less likely to be scanned. However, the worm uses an operating system service, GetTickCount, to seed their generator with the number of milliseconds since boot time, which should provide sufficient randomization to ensure that across many instances of the worm, at least one host will probe each address at some point in time. We feel confident that the risk of bias in our measurements is similarly minimized.
An interesting feature of this PRNG is that it makes it difficult for the Internet community to assemble a list of the compromised Internet addresses. With earlier worms, it was sufficient to just collect a list of all addresses that probed into a large network. With Sapphire, one would need to monitor networks in every cycle of the random number generator for each salt value to have confidence of good coverage.
Measurements of Sapphire's Spread and Operator Response
By passively monitoring traffic (either by sniffing or sampling packets or monitoring firewall logs) on a set of links providing connectivity to multiple networks, each responsible for about 65,000 IP addresses, we were able to infer the worms overall scanning behavior over time. Sapphire reached its peak scanning rate of over 55 million scans per second across the Internet in under 3 minutes. At this rate, the worm would effectively scan over 90 percent of the entire Internet in a little more than 10 minutes. This aggregate scanning rate is confirmed by all datasets with known address space coverage.
Our most accurate data describing the early progress of the Sapphire worm was obtained from the University of Wisconsin Advanced Internet Lab, where all packets into an otherwise unused network (a "tarpit" network) are logged. Since this data set represents a complete trace of all packets to an address space of known size, it allows us to accurately extrapolate the global spread of the worm. Unfortunately, a transient failure in data collection temporarily interrupts this dataset approximately 2 minutes and 40 seconds after Sapphire began to spread. Our other, sampled datasets are not sufficiently precise for accurate evaluation over short durations.
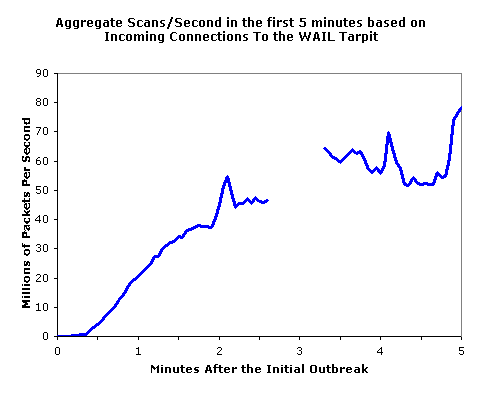
Figure 4:
The early progress of Sapphire, as measured at the University of
Wisconsin Advanced Internet Lab (WAIL) Tarpit.
In general, the response to Sapphire was quick. Within an hour, many sites began filtering all UDP packets with a destination port of 1434. Sapphire represents the idealized situation for network-based filtering: the worm was easily distinguished by a signature that is readily filterable on current hardware and it attacked a port that is not generally used for critical Internet communication. Thus almost all traffic blocked by these filters represents worm-scanning traffic. If the worm had exploited a vulnerability in a commonly used service (e.g. DNS at UDP port 53 or HTTP at TCP port 80), such filtering could have caused significant disruption to legitimate traffic with resulting denial-of-service more harmful than the worm itself.
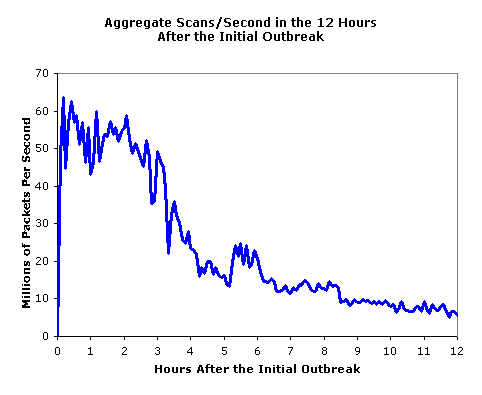
Figure 5: The response to Sapphire over the 12
hours after release, measured in several locations.
Even with optimal conditions for filter efficacy, it is important to recognize that while filtering controlled the unnecessary bandwidth consumption of infected hosts, it did nothing to limit the spread of the worm. The earliest filtering was initiated long after the worm had infected almost all of the susceptible hosts.
We recorded all distinct infected IP addresses seen by our monitors in the first 30 minutes of worm spread. Most of these machines were actually infected in the first few minutes, but due to monitoring limitations, we can't tell precisely when they were infected. We cannot observe all infected machines due to the flaws in Sapphire's PRNG, but we document a lower-bound on the number of compromised machines based on the IP addresses we have recorded -- the actual infection is undoubtedly larger. We noticed 74,856 distinct IP addresses, spread across a wide range of domains and geographic locations.
|
| ||||||||||||||||||||||||||||||||||||||||||||
| Table 1: Sapphire's geographic distribution | Table 2: Sapphire's distribution among top level domains |
Implications and Conclusions
Although some of the authors have predicted the possibility of high speed worms [5], Sapphire represents the first such worm released into the wild. Microsoft's SQL Server vulnerability was particularly well suited for constructing a fast worm (since the exploit could be contained in a single UDP packet). However, techniques exist such that any worm with a reasonably small payload can be crafted into a bandwidth-limited worm of a similar nature. Thus, the extreme speed should not be viewed as an aberration due to the nature of the exploit or the particular protocol used (UDP vs TCP).
One implication of this advance is that smaller susceptible populations are now vulnerable to attack. Formerly, small populations (<20,000 machines or less on the Internet) were not viewed as particularly vulnerable to worms, as the probability of finding a susceptible machine in any given scan is quite low. However, a worm which can infect a population of 75,000 hosts in 10 minutes can similarly infect a population of 20,000 hosts in under an hour. Thus, exploits for less popular software present a viable breeding ground for new worms.
Since high-speed worms are no longer simply a theoretical threat, worm defenses need to be automatic; there is no conceivable way for system administrators to respond to threats of this speed[5][7]. Human-mediated filtering provides no benefit for actually limiting the number of infected machines. While the filtering may mitigate the overhead of the worm's continuing scan traffic, a more sophisticated worm might have stopped scanning once the entire susceptible population was infected, leaving itself dormant on over 75,000 machines to do harm at some future point. Had the worm's propagation lasted only 10 minutes, it would likely take hours or days of effort simply to identify the attack, and many compromised machines could never be identified.
Though very simple, Sapphire represents a significant milestone in the evolution of computer worms. Although it did not contain a destructive payload, Sapphire spread worldwide in roughly 10 minutes causing significant disruption of financial, transportation, and government institutions. It clearly demonstrates that fast worms are not just a theoretical threat, but a reality -- one that should be considered a standard tool in the arsenal of an attacker.
[1] See http://www.microsoft.com/security/slammer.asp.
[2]: For complete disassembles of the worm see http://www.nextgenss.com/advisories/mssql-udp.txt, http://www.boredom.org/~cstone/worm-annotated.txt, http://www.snafu.freedom.org/tmp/1434-probe.txt, http://www.immunitysec.com/downloads/disassembly.txt, and http://www.eeye.com/html/Research/Flash/sapphire.txt.
[3] David Moore, Colleen Shannon, Jeffery Brown, Code-Red: a case study on the spread and victims of an Internet worm, Proceedings of the Second the ACM Internet Measurement Workshop, 2002.
[4] See
http://www.digitaloffense.net/worms/mssql_udp_worm/internet_health.jpg
has a single snapshot, while Tim Griffin has plotted RouteViews data
on BGP to show a substantial perturbation, available at http://www.research.att.com/~griffin/bgp_monitor/sql_worm.html.
[5] Vern Paxson, Stuart Staniford, and Nicholas Weaver,
How to 0wn
the Internet in Your Spare Time, Proceedings of the 11th USENIX
Security Symposium (Security '02).
[6] David Moore, Network
Telescopes: Observing Small or Distant Security Events, Invited
presentation at the 11th USENIX Security Symposium.
[7] David Moore, Colleen Shannon, Geoffrey Voelker and
Stefan Savage, Internet
Quarantine: Requirements for Containing Self-Propagating Code, to
appear in Proceedings of the 2003 IEEE Infocom Conference, San
Francisco, CA, April 2003.
[8] DShield: Distributed Intrusion Detection System. www.dshield.org.
Many thanks to Dave Plonka (University of Wisconsin-Madison
Division of Information Technology (DoIT) and the Wisconsin Advanced
Internet Lab (WAIL)), Pat Wilson (UC San Diego), Brian Kantor (UC San
Diego), and Johannes Ullrich and the SANS Institute for contributing
data sets for our analysis. Thanks to Lea Kissner (CMU) and David
Wagner (UC Berkeley) for help with the PRNG. We are grateful to Ryan
Koga (CAIDA) and Jeffrey Brown (UCSD CSE) for geographically mapping
the spread of the worm.
Support for this work was provided by NSF, DARPA, Silicon Defense,
Cisco Systems, AT&T, NIST, and CAIDA members.
Acknowledgments