NeTS-FIND: Greedy Routing on Hidden Metric Spacesas a Foundation of Scalable Routing Architectures without Topology Updates
The ultimate goal of this NeTS-FIND project is to find the hidden spaces underlying real networks and to identify node coordinates in them. please see the NeTS-FIND proposal in PDF.
Principal Investigators: Dmitri Krioukov kc claffy
Funding source: CNS-0722070 Period of performance: October 1, 2007 - September 30, 2010.
Project Summary
A growing consensus among experts is that the routing system is approaching a critical architectural breaking point [1] which any significant deployment of IPv6 will only exacerbate. The issue has recently drawn so much concern from engineering, operational, and policy communities that the Internet Architecture Board [2] held a workshop in November 2006 trying to identify the factors that limit routing scalability, and formulate a coherent statement of the problem [1]. Their conclusion was expected: the most acutely scale-limiting parameter of the current routing system is routing table size, not so much for its memory requirements as for its reaction to network dynamics. Specifically, topology changes require recalculation of routing tables, a computational burden as well as a performance hit since traffic is often delayed or even lost as nodes converge to the updated routing state.
Already having articulated the need for a fundamental reexamination of the routing and concomitant addressing architecture, our previous NeTS proposal allowed us to rigorously examine and evaluate known routing schemes in pursuit of one that would work on Internet-like scale-free topologies without a radical architectural shift. We learned that there are no existing dynamic routing schemes with reasonable scalability bounds on Internet-like graphs. Our current work [3], augmented with a theoretical proof in [4], offers the ominous but definitive lesson: to scale efficiently and indefinitely, we must learn how to route without topology updates.
Updateless routing seems impossible at first glance, but neighboring disciplines offer inspiration. Milgram's 1967 experiment [5], a social network exercise in letter delivery reflected in the 1990 popular play "Six Degrees of Separation" [6], demonstrated that routing in a dynamic evolving network is possible without updates. Kleinberg [7,8] provided the first formal model of such greedy routing, demonstrating its success with neither updates nor a full view of topology. But his graph construction method yielded topologies vastly different from scale-free topologies of observed complex networks, leaving open the question of whether greedy routing is the panacea it portends.
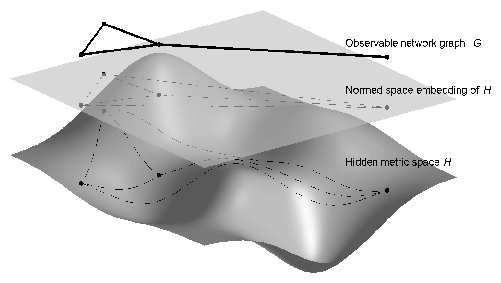
We propose a new model of Greedy Routing on Hidden Metrics, the GROHModel, that generalizes the Kleinberg model and naturally yields scale-free topologies. Our model employs the concept of a hidden metric spaces (HMSs) existing behind every complex network, including the Internet. We will thoroughly investigate the hypothesis that the observable scale-free structure of complex networks is a consequence of natural evolution that maximizes efficiency of greedy routing on these HMSs. By efficiency we primarily mean the delivery success ratio and its resilience to link/node failures. Then, as soon as we find the Internet's HMS, we can use it in addressing architectures rendering greedy routing strategies efficient.
Our research agenda includes three clearly defined tasks: (1) demonstrate the existence of HMSs; (2) build methodologies to explicitly re-construct the HMS for the observable Internet topology, and more generally for any given complex network; and (3) address challenges associated with using GROHModel-based routing in practice. We offer not only a strategic high-level program whose goals precisely match those of the NeTS-FIND solicitation, but also a detailed outline of specific research steps that we will undertake.
Intellectual Merit. The proposed research involves concerted cross-fertilization across fields of networking, theoretical computer science, physics, and mathematics. We propose to develop a novel network modeling methodology that is elegantly generic in nature, mathematically sound, and promises a solution to one of the most challenging problems of future large-scale networking.
Broader Impact. Proved faithful to reality, the GROHModel will represent a rigorous mathematical foundation for truly scalable routing architectures in dynamic networks. The models and results of this project will dramatically increase fundamental understanding of the global structure and function of not only traditional data networks, but also of many other types of self-evolving large-scale complex systems, such as biological, social, and language networks [9].
1 Introduction
Although there is no formal analysis of scalability limits for the current Internet routing system-itself a problem for researchers, engineers, policymakers and investors-there is growing consensus among experts that the routing system is approaching an architectural breaking point [1] which any significant deployment of IPv6 will only accelerate. The issue has recently drawn so much concern from engineering, operational, and policy communities that the Internet Architecture Board, charged with oversight of the technical and engineering development of the Internet [2], held a workshop in November 2006 to try to identify the factors that limit routing scalability, and articulate a coherent statement of the problem [1]. Their conclusion was expected: the most acutely scale-limiting parameter of the current routing system is routing table size, not so much for its memory requirements as for its role in dealing with network dynamics. Specifically, topology changes require recalculation of routing tables, a computational burden as well as a performance hit since traffic is often delayed or even lost as nodes converge to the updated routing state.
Already having accepted the need for a fundamental reexamination of the routing and concomitant addressing architecture, in our previous NeTS proposal we rigorously examined and evaluated known routing schemes in pursuit of one that would work on Internet-like topologies without a radical architectural shift. Our conclusion was clearer than it was auspicious: we learned that there are no existing dynamic routing schemes with reasonable scalability bounds on Internet-like graphs. The problem is routing update messages percolating through the network to announce a topology change. Our current work [3] discussed in Section 2, augmented with a theoretical proof in [4], offers the ominous but definitive lesson: if we want routing to scale efficiently and indefinitely, we must learn how to route without updates.
Updateless routing seems impossible at first glance, but neighboring disciplines offer inspiration. Milgram's 1967 experiment [5], a social network exercise in letter delivery reflected in the 1990 play "Six Degrees of Separation" [6], demonstrated that routing on a dynamic network is possible without updates. Kleinberg [7,8] provided the first formal model of such greedy routing, rigorously demonstrating its success with neither updates nor a full view of topology. But his graph construction method yielded topologies vastly different from observed complex networks, leaving open the question of whether greedy routing is the panacea it portends.
Armed again with brilliant insights from neighboring disciplines as well as our own research results, we propose to rigorously investigate the following proposition: Behind every complex network, including the Internet, there exists a hidden metric space. The observable scale-free structure of the network is a consequence of natural network evolution that maximizes efficiency of greedy routing on this metric space. By efficiency we mean delivery success ratio and its resilience to link/node failures. Our proposed GROHModel (Greedy Routing on Hidden Metrics) is a generalization of Kleinberg's model to Internet graphs, and integrates the notion of a hidden metric space. If the GROHModel faithfully reflects reality, then we can use the hidden metric space, once we find it, to build efficient updateless routing strategies for the Internet.
Our agenda has three clearly defined tasks, illustrated in Figure 2: (1) Demonstrate the existence of hidden metric spaces (HMS); (2) deliver methodologies to explicitly re-construct an HMS based on an observable graph of the Internet topology in particular, and in general for any given complex network; (3) address immediate practical problems associated with greedy routing via HMSs that must be solved before serious discussion of deployment. This research agenda, grounded in a mathematically rigorous framework, follows up on the discoveries from our previous project. We offer not only a strategic high-level program, but also a detailed outline of specific research steps needed to pursue this agenda.
2 In pursuit of scalable routing
The area of computer science that explicitly aims at developing scalable routing algorithms is compact routing. In this section we provide necessary background on compact routing, describe our recent and current preliminary results related to compact routing, and identify a fundamental obstacle on our path to truly scalable routing architectures.
2.1 Scalable routing on static topologies
Compact routing deals with construction of routing algorithms (a.k.a. schemes) such that node addresses (a.k.a. labels), routing table sizes (a.k.a. memory space or space), and stretch are all as small as possible. Stretch is the relative increase of lengths of paths produced by the routing algorithm, compared to the shortest path lengths. More formally, a routing algorithm is compact if address sizes grow no faster than polylogarithmically with network size, routing table sizes are sublinear, and stretch is constant. Note that there is an inherent trade-off between space and stretch: space compression is achieved by abstraction or aggregation, which costs details of the topology. Losing such details can only increase path lengths.
Compact routing schemes are universal if they work correctly on all graphs or specialized if they guarantee bounds only on graphs from specific graph families. The first universal optimal compact routing scheme was due to Thorup and Zwick [10]. We analyzed the performance of this scheme on scale-free graphs in [11] and found that these graphs yielded essentially the best possible performance of the scheme compared to all other graphs. Inspired by this first indication that scale-free graphs are optimally structured for high-performance routing, several research groups have independently constructed specialized routing schemes [12,13] designed to utilize structural peculiarities of scale-free graphs in order to improve performance guarantees. The schemes in [12,13] achieve polylogarithmic space and infinitesimally small stretch on scale-free graphs.
Compact routing schemes are also classified as name-dependent or name-independent. The former label the nodes with addresses embedding topological information in them, i.e., "addressing follows topology" [1]. The latter work on graphs with arbitrary node labels, i.e., node addresses can be taken from any flat address space, with no association between addressing and topology.
In our work [3], which is a part of our previous NeTS-NR project [14], we investigate the performance (space, stretch, and communication complexity) of both name-dependent and name-independent schemes. Specifically, we focus on two name-dependent schemes, by Cowen [15] and Brady and Cowen (BC) [12]. The former is universal, while the latter is specialized: it is designed specifically for Internet-like topologies. The two name-independent schemes we consider are by Arias et al. [16] and a more recent optimal improvement by Abraham et al. [17]. Both schemes are universal; we are not aware of any name-independent scheme specialized for scale-free graphs. We study the performance of these schemes both on synthetic power-law graphs [18,19] and on the best available Internet topology data measured by skitter [20], DIMES [21], and Routeviews [22]. Table 1 reports the two most important characteristics, average space and stretch, of the best performing schemes from our list. We find that the BC scheme appear to work extremely well on measured Internet topologies, yielding remarkably low values of space and stretch. This algorithm guarantees a maximum routing table size of O(log2 n) on scale-free networks, where n is the total number of nodes in the network. The O(log2 n) scaling means that even if all 2128 IPv6 addresses are totally de-aggregated and used as flat identifiers, the maximum routing table size in such an Internet would still contain not more than 1282 ~ 16,000 entries. The corresponding limit for IPv4 is ~ 1,000, two orders of magnitude smaller than today.
| Scheme | skitter (9204 nodes) | DIMES (13931 nodes) | ||
| BC | 22 entries (1025 bits), | 1.06 stretch | 22 entries (1103 bits), | 1.03 stretch |
| Abraham | 6307 entries (279218 bits), | 1.35 stretch | 8103 entries (380475 bits), | 1.45 stretch |
The exceptional performance of compact routing schemes on static topologies motivates the question: will they work on dynamic networks?
2.2 Scalable routing on dynamic topologies
Among other less fundamental concerns, the limiting assumption of all compact routing schemes to date is that the network is static. More precisely, it is not that the network is static per se, but that the algorithm requires the full view of the graph representing the network topology at any given time. Any topology change yields a new graph, on which the algorithm might have to calculate paths from scratch.
Being static, the schemes we analyze in [3] do not provide any non-trivial guarantees concerning convergence characteristics, e.g., number of control messages per topology change, etc. The only way to estimate these parameters is via simulations of truly distributed implementations, e.g., in ns2, of these schemes on realistic topologies. These simulations comprise the last portion of our current work [3]. Given the static nature of the considered schemes, we do not expect performance on dynamic graphs to be encouraging.
We recognize that the convergence problem is a crucial breaking point not only for all theoretical routing algorithms, but for practical routing methods employed in today's Internet as well. Link-state algorithms, typically used for intra-domain routing, require each node to have a consistent complete view of the network, while distance- or path-vector algorithms need each node to know only distances or paths to all other nodes.1 Since in the worst case any node might be asked to forward a packet to any destination, all nodes must have a coherent complete view of the network topology, or at least some of its partitions. In order to achieve such a coherent full view, timely topology update messages, a.k.a. routing updates, seem unavoidable. Updates require recalculation of routing tables and lead to delay, instabilities, churn, and other complications [24,25,26,27,28,29]. Long convergence times are both a critical problem and an absolutely inevitable implication of scaling the current routing architecture [1].
One of the popular proposed solutions to the convergence problem is the idea of splitting two functions currently served simultaneously by the IP address: locator and identifier. The idea is that in an architecture where one label identifies a node and a different label indicates its location, topology changes will only change the locators, but routing can use the identifiers. Unfortunately, a locator-identifier split means that in addition to updating locators as before, nodes must also maintain and update a proper locator-to-identifer mapping somehow, a burden unlikely to improve scaling characteristics. Indeed, Table 1 shows that name-independent schemes, which all provide a form of locator-identifer splitting, scale more poorly than name-dependent ones in both routing table size and stretch. The observable reality is that locator-identifier split comes at quite a scalability price.
Yet more pessimistic results come from the the theoretical computer science community. Using fairly general arguments, Afek et al. [30] showed that the worst-case number of updates per topology change cannot be lower than W (n) where n is the number of nodes in the network. After seventeen years of virtually no progress, Korman and Peleg [4] have recently tried to improve this pessimistic lower bound. Unfortunately, their result is even more pessimistic than Afek's. Indeed, they show the worst-case number of updates per topology change cannot be lower than W (D) where D is so-called local density, a characteristic related to the distance distribution of a graph, but one can check that D is of the order of n for small-world topologies, such as the Internet (cf. Section 3). In other words, recent work [4] definitively implies that in terms of routing churn, Internet-like graphs are as bad as the absolutely worst-case graphs across all possible network topologies.
We are at an apparent impasse. Updates and associated convergence appear to be an unavoidable element of the routing process, but theoretical analysis shows that they are the fundamental obstacle to acceptable routing scalability. While routing table sizes and stretch produced by compact routing schemes are overwhelmingly small on static topologies, these schemes cannot guarantee scalable convergence behavior. That is, we get blocked on the network dynamics problem and must face the reality that scalable routing which uses topology update messages to dynamically react to topology changes is not possible in principle. In order to resolve the dynamics problem we need some radically new ideas.
3 Routing without topology updates
As heretical as it sounds, the best available data on Internet topology and our best understanding of routing implies that the only possible path to true routing scalability is to have no updates at all. At first glance, removing updates suggests that nodes will not know where destinations move, forcing a retreat to either flooding or random walks, both completely unscalable. However, Milgram's experiments prove such desperation premature by giving us a cue to where a solution to scalable routing might be hiding.
In 1967, Stanley Milgram [5] asked a few randomly selected individuals in Nebraska to send letters to a randomly selected person, a stock broker in a suburb of Boston. The letters had the destination address visible consisting only of the name of the stock broker, his occupation, and the city he lived in. Milgram specified one routing restriction: each source and intermediate node had to forward a packet only to his/her friend that, in the current node's opinion, maximized the probability of moving the packet closer to the destination. Approximately 30%2 of packets reached the destination using an unexpectedly low number of hops. The average hop length of letter paths was about six [6].
Milgram's experiments illustrate that humans can route messages efficiently among each other without topology updates, and consequently without the full view of the topology. Each node's view is ultra-local; it sees only its neighbors, i.e., his/her friends, and maybe a few neighbors of its neighbors. However, addressing in this topology is remarkably clever, as nodes are informatively and succinctly labeled, i.e., node addresses are combinations of place of living, occupation, etc. Given this local view of the global topology and the informative labeling scheme, a node can route greedily by efficiently estimating who among its neighbors is closest to the destination.
Insights from Milgram's experiments have recently received renewed attention from computer science and physics researchers analyzing their implications. The first popular model aiming to formalize and explain the success of Milgram's experiments was by Kleinberg [7,8], inspired by the first small-world model by Watts and Strogatz [32]. Nodes reside in a metric space, which is a two-dimensional grid in the original Kleinberg model. The distance between two nodes in this space represents "intrinsic similarity" between them, e.g., "social similarity" between humans. The network topology graph consists of edges, i.e., connections between pairs of nodes. The closer two nodes are to each other in the grid, the higher the probability that they are connected. The connected nodes are called neighbors. No node has the full view of the network topology. Each node knows only its coordinates in the grid and the coordinates of its neighbors. Equipped only with this information, nodes can route efficiently in a greedy manner-by forwarding packets to their neighbors closest to the destination, where "closest" refers to the grid distances, not to the distances in the network topology graph.
The Kleinberg model is a fantastic contribution to our theoretical understanding of routing, but the looming problem is that his graph construction method yielded topologies vastly different from observed complex networks, leaving open the question of whether greedy routing is applicable to Internet-like, i.e., scale-free topologies-the question we seek to answer.
Topology matters to routing [11,33]. One cannot hope to find optimally scalable routing solutions without understanding of the underlying topology. In particular, there are graphs such that no addressing would simultaneous allow for successful greedy routing and be succinct [34], i.e., it would always require keeping significant parts of the full view at each node, preventing small routing table sizes. Topology is thus crucial, and an explanation of greedy routing efficiency in Milgram's experiments should directly exploit peculiarities of the structure of networks involved.
Interestingly, not just the Internet topology, but topologies of many social, communication, and biological networks are scale-free [9], which most researchers agree involves two properties: heavy-tailed node degree distributions that often follow power laws, and strong clustering, i.e., high probability that a pair of neighbors of the same node is connected. An important consequence of the power-law property of scale-free networks is that they are small-world: their average shortest path lengths, and in fact lengths of most paths, are extremely small. The average distance of the AS-level Internet is 3.5 [35], and rigorous results show that average distances in power-law graphs cannot grow faster than logarithmically with the number of nodes [36,37]. In previous work [11,33] we showed that small-world graphs render inapplicable all attempts to fix routing scaling problems by means of "aggressive aggregation" [1] or other synonyms of hierarchical routing [23].
Our albeit intellectually rich foray into compact routing effectively tackled the problem of routing on scale-free graphs, but only static ones. Our awareness that we need to cope with dynamic scale-free graphs, Korman and Peleg's recent result [4] on the scalability limitations of update-based routing, and finally Milgram's positive results for greedy routing on social topologies that share fundamental characteristics with the Internet, strongly motivate us to vigorously pursue Kleinberg's ideas in the context of future Internet routing architectures. The work we propose next seeks to answer the looming question: can we construct a scalable routing and addressing architecture for the Internet that does not require a complete view of the topology? We now introduce the model that comprises our approach.
4 GROHModel: Greedy Routing on Hidden Metrics
Armed with results from Milgram, Kleinberg, and a long legacy of struggles to improve routing efficiency, we propose to rigorously investigate the following hypothesis: Behind every complex network, including the Internet, there exists a hidden metric space. The observable scale-free structure of the network is a consequence of natural network evolution that maximizes efficiency of greedy routing on this metric space. We call our model the GROHModel for Greedy Routing on Hidden Metrics.
The logic and intuition leading us to this hypothesis are rooted in the following observations. The main function of complex networks is to serve as efficient substrates for dynamic processes running on them. Therefore, topological structure of complex networks and their scale-free organization are plausible consequences of self-evolving optimization toward such efficiency. In particular, processes running on complex networks are often information propagation and dissemination. That is the case for communication networks, e.g., the Internet, and social networks, and also applies to biological networks, such as neural networks, signaling pathways, and even metabolic networks.3 In most cases this information propagation is "blind," akin to diffusion, and not designed by humans but done by nature. Yet the dissemination process is still efficient and properly targeted, i.e., there is an implicit concept of destination that pure diffusion lacks. The most natural formalization of this type of targeted diffusion is greedy routing over metric spaces where distances represent relative functional or structural similarity among individual objects, i.e., nodes. We call these metric spaces hidden as they are not immediately observable, but rather manifest themselves indirectly via observable properties and structures of network graphs built "on top" of these spaces according to certain generation algorithms.
To formalize the proposed GROHModel we introduce the following definitions:
Hidden metric spaces (HMSs). All nodes x I
V,
|
V|
=n reside in a hidden metric space H,
meaning that in this space every two nodes x,y I
V are located at
a distance r
(x,y) from each other.
The distance possesses the following three
properties: 1) r
(x,y) 3
0; 2) r
(x,y) = 0U
x = y; 3) r
(x,y) = r
(y,x);
4) r
(x,z) L
r
(x,y) + r
(y,z).
Taken together, all pair-wise distances form a distance
matrix r
, which fully specifies H.
Connection probability. Observable graph G(V,E) is
formed by creating links between every pair of nodes x,y I
V with probability p(r
(x,y)), where p is a decreasing function.
Since this function is decreasing, strong clustering in scale-free
networks finds an immediate explanation in the GROHModel. Indeed,
according to the triangle inequality property of H, any two
nodes that are close to the same node are also close to each other,
and thus links between all three of them exist with high probability.
Greedy routing. Let n
i, i = 1 1/4
k be all neighbors of node x of degree k, i.e.,
(n
i,x) I
E. Given a destination z, greedy routing
strategy at x forwards a packet to neighbor n
s such that
r
(n
s,z) = mini=1 1/4
k(r
(n
i,z)).
We will estimate the efficiency of greedy routing in terms of space, stretch, and resilience.
Space. Greedy routing requires each node to know its hidden distance, along with the distances from all of its neighbors to every destination. The trivial space requirement at k-degree node x is therefore O(kn) and its upper bound over all nodes is O(kmax n), where kmax is the maximum degree in the graph. If we can embed H into a normed space of a constant low-dimension d, cf. Section 5.2.1, then the corresponding bounds drop to O(kd) and O(kmaxd), i.e., the routing table size of the node becomes simply proportional to its degree.
Stretch. We define the following stretch-based metrics:
Success ratio. In a general setting, greedy routing does
not guarantee delivery for every source-destination pair. We define
the success ratio s(x) of a source node x as the fraction of
nodes that greedy routing can reach from x. Its average over all
source nodes is the overall success ratio s. We call
source-destination pair (x,y) succeeding if greedy
routing finds a path from x to y.
Visible stretch. Let d(x,y) be the shortest
path distance, measured in graph G, between nodes x and y, and
let d
(x,y) be a distance, also measured in G, of the
succeeding routing path from x to y. The visible stretch of this
path is sv(x,y)=d
(x,y)/d(x,y), and the average
observable stretch is its average over all succeeding paths.
Hidden stretch. Let the succeeding path from x to y in
space H be (v0, v1, 1/4
, vd
(x,y)), v0 = x
and vd
(x,y) = y. The hidden stretch of this path
is sh(x,y) = a
i=1d
(x,y)r
(vi-
1,vi)/r
(x,y), and the average hidden stretch is its
average over all succeeding paths.
Resilience. In case of link or node failures, the number of node pairs that cannot reach eachother can only increase. To measure the degradation of stretch-based characteristics upon various scenarios of link or node removal we will employ a series of resilience characteristics, e.g., average or maximum (relative) decrease of success ratio per random link or node failure, etc.
We can now express the GROHModel hypothesis more formally: combinations (H,p) of HMSs H and connection probabilities p, which lead to scale-free topologies of observable graphs G, maximize efficiency of greedy routing, measured primarily by the delivery success ratio and its degradation upon link or node failures.
5 Proposed work
Figure 2 illustrates our work plan. The proposed work consists of three tasks:
- Demonstrate the existence of hidden metric spaces.
We will validate that the GROHModel reflects reality. We will reveal generic structural properties of hidden metric spaces that would simultaneously: i) maximize greedy routing efficiency according to the metrics from Section 4; and ii) produce scale-free graphs. - Find these spaces.
We will deliver methodologies to explicitly re-construct an HMS based on an observable Internet graph in particular, and in general for any given complex network. - Address challenges associated with using GROHModel-based routing in practice.
We will identify and evaluate immediate challenges associated with implementing GROHModel-based routing architectures in practice, and develop simple and efficient techniques dealing with such challenges.
We further split these tasks into subtasks and show them as numbered boxes in Figure 2. We refer to these box numbers as "box #a.b.c," to simplify navigation through our proposed work plan.
5.1 Task 1: The GROHModel validation
Our validation strategy is two-part. First, we will conduct simulations to test several metric space models as candidates for GROHModel HMSs, i.e., we fill find such combinations of metric spaces and connection probabilities that simultaneously maximize greedy routing efficiency and lead to scale-free topology formations. We will then try to prove these findings analytically and provide analytic estimates of greedy routing performance metrics.
5.1.1 Simulations
We will experiment with different metric space models using the following three-step methodology: (i) construct metric spaces H according to a given model and calculate their distance distributions; (ii) construct observable graphs G, calculate their properties, and compare them with observed topologies; and (iii) evaluate resulting greedy routing performance.
To analyze the topology of the modeled graph G and to compare it with observed topologies, we will use the dK-series approach [41] developed in the course of our previous project [14]. Since our model graphs G are built on top of HMSs, we will measure correlations between hidden distance distribution-based and dK-series-based metrics, such as correlations between average distance from a node in H to all other nodes and the average degree of the same node in G. We will also measure the density of links in G as a function of distance in H between nodes they connect. This link density is particularly important because all Kleinberg models have approximately uniform density of edges connecting nodes located at different distance scales [42].
In case our analysis becomes computationally intensive, we will use compute resources of the San Diego Supercomputer Center where we are conveniently located.
Three initial plausible classes of HMS candidates for the GROHModel are: normed spaces, random metric spaces, and expanding metrics .
Normed spaces, box #1.1.1. Normed spaces lpd are the simplest candidates [43,44]. They are spaces of d-dimensional real vectors x I \mathbbRd with the lp norm | x| p = (a i=1d xip )1/p, where p 3 1 is an integer. The lY norm is | x| Y = maxi| xi| . Normed spaces are metric spaces with metric function r (x,y)=| x- y| p.
Motivated by a continuum version of the Kleinberg model in [45], we have already started initial experiments with the GROHModel on the Euclidean plane, the simplest normed space, and found that the resulting graphs are scale-free and maximize greedy routing efficiency only if node concentration in the plane is scale-free, i.e., if node density per unit square is a power-law function of the distance from the origin. This preliminary result is encouraging, but we suspect that Euclidean spaces are not good candidates for Internet HMSs since they cannot produce disassortative4 graphs [47], such as the Internet [35].
Another concern with Euclidean spaces is that they are rather "restrictive" [43,44]. They form only a tiny portion of all metric spaces. In particular, random metric spaces do not embed into them with high probability [48].
Random metric spaces, box #1.1.2. Vershik [48] introduces an explicit model of random metric spaces [49] and specifies an algorithm to iteratively grow random distance matrices. At each step, i.e., when the n'th node is added to the space, the distance between the n'th and first nodes is independently selected according to some probability distribution x on \mathbbR+, e.g., normal, exponential, power-law, etc. The distances between n'th and all other nodes are selected uniformly at random from the set admissible by the triangle inequality. This process yields an ensemble of growing distance matrices parameterized by x . Vershik then shows that regardless of x , such an ensemble ultimately defines an infinite metric space that is everywhere dense in the Urysohn space [50], which is the unique universal random metrics space, meaning that all "sufficiently random" metric spaces embed in this space isometrically.
We have performed initial experiments with Vershik spaces and obtained encouraging results that among all possible distributions, only power-law distributions with exponents close to those observed in power laws of real scale-free networks produce distance distributions that are approximately uniform for short distances. This result is encouraging because it is exactly this distance property that maximizes the success of greedy routing at small distances [51], which is the hardest scale for greedy routing to handle well.
Expanding metrics, box #1.1.3. The metric spaces discussed above are static, which does reflect the reality of growing networks. We will experiment with dynamic modifications of existing metric space models. In particular, we will investigate the Aldous model [52,53], in which the hidden distances between a new node and existing nodes are independent exponentially distributed random variables. Observable links to other nodes are created with probability which is an exponentially decreasing function of the distance in the current-state HMS, and with hidden distances that grow exponentially as the network evolves. The Aldous model is analytically tractable and produces scale-free graphs, but does not consider routing, so our first step with expanding spaces is to test greedy routing on the unaltered Aldous model.
We recognize that the three classes of metric spaces listed in this subsection do not exhaust all possibilities. Spaces that simultaneously maximize greedy routing efficiency and form scale-free observable graphs, i.e., GROHModel HMSs, may even contain elements of all three and possibly some other ingredients, box #1.2.2.
5.1.2 Analysis, box #1.2.1.
Rigorous analysis of scale-free graphs has proved notoriously difficult [36]. While several different approaches are available for analytic GROHModel validation, we currently favor the approach based on hidden variables [54] by Boguñá and Pastor-Satorras. Their hidden variable methodology proved surprisingly efficient in simplifying complicated calculations, including calculations of distance distributions in power-law graphs [55] and of various properties of preferential-attachment networks [54]. Besides being a powerful tool for complex network analysis, hidden variables naturally fit the GROHModel formalism. We have established collaboration with Boguñá and already obtained preliminary encouraging results indicating that greedy routing resilience to random link failures is maximized for exactly the same (H,p)-combinations as those giving rise to observed scale-free topologies.
5.2 Task 2: Finding hidden metric spaces
The output of Task 1 is ensembles of hidden metric spaces (HMSs) and connection probabilities such that their combinations give rise to scale-free graphs maximizing greedy routing performance. Task 2 is to find a specific HMS for a concrete network, in our case the Internet. Completing this task will prepare us to construct efficient addressing schemes based on this HMS.
We see two independent solution paths for this challenging task (Figure 2): the conceptually simpler but practically more difficult generic path, and the more complex but easier to actually follow explanatory path. Results from the generic path will be elegantly applicable to any scale-free network. Results on the explanatory path are specific to a given network but also offer useful and potentially fundamental insights about that network and its evolution.
5.2.1 Generic path
Given a concrete measured topology G of a given network, e.g., the Internet, and its underlying candidate H, we will find an explicit fit of G into H, box #2.1.1, using the correlations between the dK-series [41] for G and distance distribution characteristics of H that we will have calculated as part of Task 1. As soon as we find such an H-G match, we have only two problems left in in Task 2: label sizes and label assignment for new nodes.
Label sizes, box #2.1.2. Suppose that we find a matching between G and H. We now need to assign labels to all nodes such that given the labels of two nodes we can quickly compute the distance between them in H. If H is a low-dimensional normed space, then label sizes will be small. However, if H is more complicated, e.g., a random metric space from the Vershik model, then we need a solution.
The trivial approach is that each node keeps the distances to all other nodes. The space requirement at k-degree node x is then O(kn) and its upper bound over all nodes is O(kmax n), where kmax is the maximum degree in the graph. This suboptimal upper bound is not better than the upper bounds of all routing algorithms used in practice today [33]. Of course, we still are much better off since without updates we no longer have churn, but this upper bound is not even sublinear.
Solution path. We use metric embeddings [43,44]. Specifically we will seek low-distortion embeddings of identified HMSs H into normed spaces of low dimensions d. Bourgain [56] showed that any n-point metric space embeds into normed spaces lpd with distortion O(logn) for any p. This distortion is the worst-case multiplicative factor mismatch between distances in the original metric space and its embedding. Abraham et al. [57] have recently decreased the minimum required dimension d for such embedding to its optimum O(logn). We will use existing techniques [43,44] to check if our HMSs allow for low-distortion embeddings into low-dimensional target spaces. We need the dimension d to be low since after the embedding the upper bound of the routing table size drops to O(kd)-node degree times the number of coordinates in a d-dimensional space. Distortion must also be low because it can only increase the stretch-based characteristics of greedy routing. In particular, the higher the distortion, the lower the success ratio, since the number of local minima grows with distortion. We discuss the problem of local minima in Section 5.3.1.
Depending on the structure of HMSs from Section 5.1, we will investigate different classes of target spaces. Besides traditional lp spaces, other likely candidates are probabilistic tree metrics, which first appeared in [58,59] and have seen rapid development since, and negative curvature metrics [60]. If we find these specific classes inadequate, we will have to retreat to generic embeddings into lp. We will use the most appropriate approach(es) from those that guarantee worst-case distortion [61,62], average-case distortion [57] or distortion with slack (a small constant portion of node pairs is allowed to have arbitrarily large distortion) [63,64].
Label assignment for new nodes, box #2.1.3. Suppose we have all nodes appropriately labeled. The problem is how new nodes joining the network can assume proper labels without global coordination or relabeling of other nodes. This problem highlights the key disadvantage of the generic path. Indeed, we believe that the GROHModel efficiency must be a natural consequence of network evolution laws, yet the generic approach totally ignores them.
Solution path. A promising solution uses local network exploration. Upon joining, a new node checks the labels of its neighbors, labels of their neighbors, and possibly other information about those nodes, e.g., degree. The GROHModel predicts that nodes are likely close in the HMS H to its neighbors in graph G. Therefore, inspection of labels in a local neighborhood in G provides information about a node's location in H. As soon as we know the key properties of H and its most efficient embeddings, we will develop techniques to infer a new node's position in H from its local connectivity in G. Relevant recent tools [65,66,67] deal with inference of global graph properties based on local inspection.
5.2.2 Explanatory path
The explanatory path is conceptually more complex, but does not have the problems associated with the generic path. This path has three stages: 1) network evolution modeling, 2) transforming a resulting model into its equilibrium counterpart, and 3) finding a hidden distance function.We emphasize that our methodology for pursuing the explanatory path is generic. Although we will test it using the AS-level Internet topology since it is the one where a scalable routing solution is most urgently needed today, our methodology is not Internet-specific.
Network evolution modeling and validation, box #2.2.1. There are many AS-level topology growth models [68,69,70,71,72,73], but we are not aware of any model that simultaneously: 1) is realistic, 2) has all its parameters measurable, 3) is analytically tractable, and 4) "closes the loop." The last requirement means that if we substitute the measured values of the parameters into analytic expressions of the model, then these expressions would yield results matching empirical observations of the real Internet. The second requirement is critical [74]: with unmeasurable parameters, one can freely tune them to match the observations, thus creating an illusion that the model "closes the loop."
During our current project [14] we constructed a model that satisfies all four requirements [75]. To validate this model, we will use our recent award-winning results on AS classification [76] and AS relationship inference [77], as well as our on-going work on extending the dK-series terminology [41] to support semantic annotations on nodes and links, such as AS type (for nodes) or AS relationship type (for links).
Finding a correspondence between a network growth model and its equilibrium counterpart, box #2.2.2. In the previous step, we identified an algorithm to grow a graph by incrementally adding nodes [75]. New nodes select target nodes to attach to, based on their attributes. For example, in the original preferential attachment growth model [78] these attributes are simply node degrees. In our evolution model [75] these attributes, in addition to node degrees, include parameters related to geographic regions and economic realities, e.g., AS type, number of customers, provider, peers, etc. The output of our growth model is a graph of n nodes, each with attributes or "pre-labels" used to build this graph one node at a time. Now we must assign new attributes (actual "labels") to the nodes such that the same graph can be reproduced via an equilibrium graph generation process that creates the whole graph of size n at once, as the GROHModel does. In this static graph generation, the probability of a link between two nodes is a function of their attributes.
We will use the hidden variable formalism [54] (cf. Section 5.1.2) for this task because it allows us to naturally transform a growth model into equilibrium ensemble of graphs with properties equivalent to the original. In particular, the authors of [54] show how hidden variables transform preferential attachment growth [78] into a static equilibrium setting. One of the key elements of this transformation is that the time a node joins a network becomes one of the hidden variables of the node. We will extend this hidden variable transformation to work with our model, and also try to extend it to apply to any generic network growth model in order to extend the applicability of the explanatory path to different network architectures.
Finding a hidden distance function, box #2.2.3. The output of the previous step is a network topology with labeled nodes. The labels will be a combination of tags related to AS's geographic position and coverage, its economic role, e.g., its AS type such ISP or customer, the time of its first appearance in the Internet, its annotated degree, etc. An AS can thus label itself locally, without any full view or topology inspection. Note that, in contrast to the generic path, labels explicitly contain routing policy information. Therefore, greedy routing on such labeled graphs will automatically satisfy policy routing constraints.
Let vector hv denote node v's label comprised of these informative tags. We now need to find a function c that, given the labels of two nodes, yields the hidden distance r between them: c (hv,hu) ~ r (v,u). We can do this using standard combinatorial optimization techniques. The last step will be to show that the c -function remains stable as the network grows. Equipped with hv-labeling and this c -function, nodes can route greedily!
5.3 Practical challenges of the GROHModel
After finding an optimal hidden metrics space or, alternatively, an equivalent hidden distance labeling scheme, we will address the following three main classes of challenges before we can consider using GROHModel-based architectures in practice.
5.3.1 Local minima escape and avoidance
Even if we find an optimal HMS, i.e., one maximizing greedy routing performance according to the metrics in Section 4, it may still not guarantee a 100% delivery success ratio. The problem is local minima : sets of nodes xt, defined for every destination t, such that none of xt's neighbors n xt is closer, in the HMS, to t than xt themselves, i.e., they are the local minima among their neighbors in the observable graph, of the hidden distance to the destination. Trivial greedy routing cannot find a path to the destination from such nodes. Furthermore, if a greedy routing path from another source hits a local minimum, it gets "stuck" there, and packets following that path get lost.
Many strategies are known to deal with local minima escape and avoidance. We will experiment with some of them and find which strategy works best in which cases. Two promising strategies are lookaheads and simulated annealing; we anticipate that techniques involving mostly lookahead-based strategies and some simulated annealing components will best handle local minima.
Lookaheads, box #3.1.1, amount to checking the path one hop further, compared with unmodified greedy routing. For example, to avoid a local minimum xt that appears, to some intermediate node n xt, as the next hop on the greedy path to t, we have n xt check if xt has a neighbor closer to t than xt itself. If xt does not have such a neighbor, n xt does not use xt as the next hop to t. We can easily implement the required checking by having xt report to all its neighbors the set of destinations t for which xt is a local minimum. So the 1-hop5 lookahead greedy routing algorithm is: forward a packet to your neighbor closest to destination t and which is not a local minimum for t. If a local minimum xt is a source of traffic to t, it suffices for xt to forward packets to its neighbor which is closest to t. Lookahead strategies have proved effective in many contexts similar to ours [80,79,81,82,83,84,66,31].
Simulated-annealing, box #3.1.2, perturbs greedy routing at node x to use its neighbor n x as the next hop to destination t with probability pn x = c exp(- D r n x/T), where D r n x = r (n x,t)- r (x,t) is the difference in distance to t, c is a normalization constant such that a n x pn x = 1, and T is temperature. If T (R) 0, we have unperturbed greedy routing. When T (R) Y , it is a random walk. Simulated annealing with any non-zero temperature guarantees findng a destination, but it might take an exponentially long time [85].
5.3.2 Network design, box #3.2.1
In certain cases, e.g., the AS-level Internet, a global network topology redesign is not an option. The topology is given-we must route on it by first finding the HMS that shaped it. In other cases, we might have the full control over the global structure of the topology. Such cases include per-ISP router-level topologies of today and visions of future Internet infrastructure as a collection of shared and programmable network hardware resources, e.g., GENI [86,87]. For these cases, we will use the GROHModel insights from Section 5.2, with improvements from Section 5.3.1, to devise algorithms for constructing both network topologies and their addressing schemes that maximize updateless greedy routing performance.
5.3.3 Loss and delay
One can design a network topology and refine it with local minimum escape and avoidance techniques, but greedy routing stretch-based metrics may still not always be optimal. Some packets can be lost or incur non-trivial delay. More beguiling, these metrics might be optimal for a given topology, but suboptimal when topology changes. Loss and delay do occur in the existing Internet, partly due to routing issues. However, it is an implicit and typically valid assumption of the existing Internet architecture that routing eventually finds all paths.
This assumption might not be safe to make in GROHModel-based routing architectures. We will find and report the limits of loss and delay, i.e., success ratio and stretch, that we must be prepared to cope with if we deploy the GROHModel with all known improvements. We will consider both the case when the topology is given, e.g., the AS topology, and the case when we can (re)design it subject to some realistic constraints, e.g., the router topology.
If loss or delay numbers are unacceptably high, we will consider three extensions to the GROHModel that use rudimentary elements of traditional routing with updates: box #3.3.1: use updates to globally distribute information about location of high-degree landmarks that low-degree nodes can use as routing proxies in case they cannot find a direct path to a destination; box #3.3.2: a hybrid model using greedy routing at large hidden distances but conventional routing protocols locally; and box #3.3.2: integration of techniques from disruption- and delay-tolerant networking (DTN) project [88] launched by SP Dr. Fall.
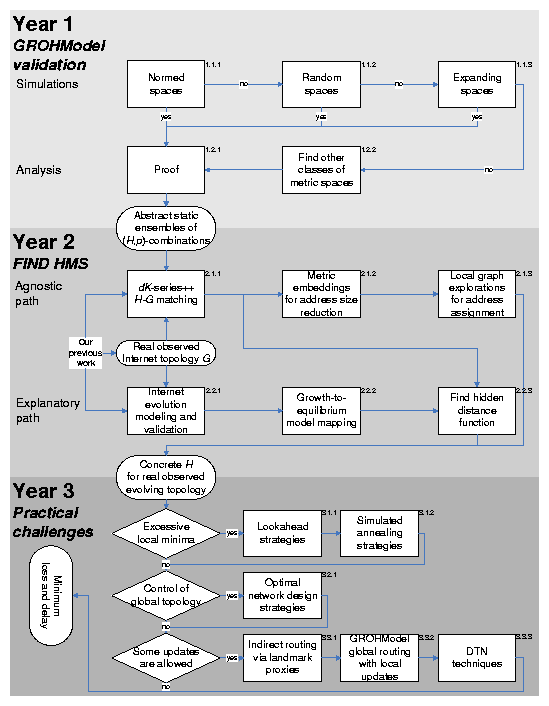 |
Figure 2: The proposed work flow.
6 Related work
We have discussed much related work in the course of describing our proposal, but other work informed our thinking without directly feeding into our proposal.
The "Pocket switching" [89,90] networking project is likely the closest in spirit to the GROHModel. It aims to build an architecture for data networking over human-held wireless devices. If successful, it will literally reproduce Milgram's experiments in the networking context. The project is currently blocked on acquiring more representative datasets of human mobility.
At the formal level, the closest areas of research are on geographic routing [91,92,93,94], P2P overlay networks [95,96,97,98,99,100,101], Internet delay distance estimation [102,103,104,105,106,107], and routing using potentials [108]. In the first three cases we have underlying metric spaces: physical space, synthetic virtual overlay spaces, e.g., toruses in CAN [95] or rings in Chord [99], and Internet delay space, respectively. Furthermore, routing is greedy in the first two cases, while in the third case the task is to find low-distortion metric embeddings as in Section 5.2.1. However, in all three cases the corresponding spaces have little in common with abstract HMSs invoked in Kleinberg models and especially in the GROHModel. As such, the former spaces, taken as is, can hardly lead to efficient greedy routing. In addition, many of them are Euclidean, which as explained in Section 5.1.1 renders them unlikely candidates for GROHModel HMSs [51,47].
Another closely related area of research is on distance labeling [109,61,34,110,111]. The task is to find node labels such that given labels of two nodes, one can quickly compute the shortest-path distance between them in the graph. The full view of the graph is assumed. The difference with the Kleinberg and GROHModel is that there is no metric space other than the one induced by shortest path lengths in the graph itself. Distance labeling on graphs is closely related to both metric embedding and compact routing research. In fact, Brady and Cowen [111] have recently demonstrated that any exact distance labeling scheme automatically yields a compact routing scheme.
7 Conclusion
Routing is a core element of any network architecture, but also the function with the greatest scaling problems. Ominously, and in fact a motivation for the FIND program, there is broad consensus that the existing Internet routing architecture has reached its scalability limits and needs to be replaced [1]. Inspired by recent developments in the theory of dynamic routing [4] and the best available data on Internet topology, we identified the most formidable obstacle on the path to scalable routing: churn. To route efficiently, nodes must know where destinations are. On dynamic networks, any distributed routing algorithm must disseminate updates upon topology changes, and recent work confirms that there is no routing algorithm that requires only a scalable amount of updates on realistic topologies. The implication is bad news for the Internet: one cannot design a truly scalable routing algorithm within the existing routing architecture. The good news is that circumstances in networking, theoretical computer science, physics, and mathematics have created a rare opportunity to pursue a fundamental breakthrough in scalable routing on real world networks.
Armed with results and collaborators from neighboring fields, we thus propose a radical shift in philosophy: updateless routing. Instead of routing to a destination, we greedily find it based on an entirely different addressing architecture. Our approach is based on hidden metric spaces (HMSs), which we claim underlie real networks, and we propose methodologies to find them. Once we find them, routing can use the metrics in these spaces to route efficiently without topology updates.
Finding and validating the power of HMSs on Internet-like topologies is an ambitious undertaking, but our research agenda is cohesive, well-considered, and mathematically as well as empirically grounded. Our new routing philosophy is also beautifully generic and applies not only to packet- or circuit-switched networks but also to any large-scale complex network architecture where nodes participate in targeted information propagation. We believe that greedy routing on HMSs is directly related to fundamental network evolution principles that lead to observable structural similarities among Internet and many other self-organizing complex networks. In other words, in our search for truly scalable routing for future global networking, we will also shed light on universal laws of evolution of complex networks-a challenge identified by the NAS as one of the highest priorities of Network Science [9].
8 Broader Impact: Outreach to the Community
The proposed work will cross-fertilize networking, theoretical computer science, physics, and mathematics, as the the proposed modeling methodology uses tools and techniques from all these disciplines. If successful it will dramatically increase our fundamental understanding of not only traditional and future data networks, but also of many other types of self-evolving large-scale systems, such as biological, social, and language networks. Our agenda is directly responsive to needs articulated by NSF in this solicitation, the NSF-sponsored workshops on theory of networked computation [112], and IAB-sponsored workshop on the future of the Internet routing system [1].
In addition to publishing our results via conferences, journals, and on the web we will present our results to network engineering and operational communities at the IETF [113] and IRTF [114] meetings, as well as in academic research venues. We will also host a routing workshop in 2007 or 2008, hoping for the same success we had with our 2006 Workshop on Internet Topology [74]
PI Dr. Krioukov is the chair of the IRTF [114] Routing Research Future Routing Scalability Working Group [115] chartered with an agenda acutely related to work proposed here. His responsibilities as chair include annual reports on the status of research covered by the working group charter [115]. He is a member of the editorial board of the ACM SIGCOMM Computer Communication Review, and a PC member of the last CoNext and next SIGCOMM. PI Dr. Claffy, is on the editorial board of IEEE Internet Computing, which has recently taken an interest in highlighting limiting architectural issues of the Internet. SP Dr. Fall is a founder and chair of the DTN Research Group [116] and a member of the IAB [2].
9 Results from Prior NSF Support
NeTS-NR Toward Mathematical Rigorous Next-Generation Routing Protocols for Realistic Network Topologies. CNS-0434996, $900,000 Oct 04 - Sep 07 (Claffy & Krioukov) This project opened a new area of research focused on applying key theoretical routing results in distributed computation to extremely practical purposes: fixing Internet routing. Our agenda had three tasks, all of which are or will be complete this year: 1) execute the next step toward construction of practical but mathematically rigorous next-generation routing algorithms; 2) validate the applicability of these algorithms against real Internet topology data; 3) build and evaluate a model for Internet topology evolution that reflects fundamental laws of evolution of large-scale networks. In the current proposal, we extensively use or build upon the works [33,35,41,76,77,74,75,3] (cf. Sections 2,5) resulted from execution of all the three tasks above.
"Correlating Heterogeneous Measurement Data to Achieve System-Level Analysis of Internet Traffic Trends," ANI-0137121, $1,000,794 Sep 2002 - Aug 2006 (Claffy) Internet Measurement Data Catalog, to cope with the most daunting challenge researchers face in studying the Internet: access to relevant and representative data on operational Internet infrastructure.
"Routing and Peering Analysis for Enhancing Internet Performance and Security," ANI-0221172, $870,999 Oct 2002 - Sep 2005 (Claffy) Topology and root cause analysis of growth and instability of the routing system, applying graph theory and combinatorial approaches to identifying strategic/vulnerable parts of the infrastructure.
References
- [1]
- D. Meyer, L. Zhang, and K. Fall (Edts.), "Report from the IAB workshop on routing and addressing." IRTF, Internet Draft, 2006.
- [2]
- "Internet Architecture Board (IAB)." http://www.iab.org/.
- [3]
- A. Brady, J. Burke, L. Cowen, K. Fall, D. Krioukov, and A. Vahdat, "Scalable routing with flat addressing." in progress.
- [4]
- A. Korman and D. Peleg, "Dynamic routing schemes for general graphs," in ICALP, 2006.
- [5]
- S. Milgram, "The small world problem," Psychology Today, vol. 1, pp. 61-67, 1967.
- [6]
- J. Guare, Six Degrees of Separation: A Play. New York: Vintage Books, 1990.
- [7]
- J. Kleinberg, "Navigation in a small world," Nature, vol. 406, p. 845, 2000.
- [8]
- J. Kleinberg, "The small-world phenomenon: An algorithmic perspective," in STOC, 2000.
- [9]
- Network Science. Washington: The National Academies Press, 2006.
- [10]
- M. Thorup and U. Zwick, "Compact routing schemes," in SPAA, 2001.
- [11]
- D. Krioukov, K. Fall, and X. Yang, "Compact routing on Internet-like graphs," in INFOCOM, 2004.
- [12]
- A. Brady and L. Cowen, "Compact routing on power-law graphs with additive stretch," in ALENEX, 2006.
- [13]
- S. Carmi, R. Cohen, and D. Dolev, "Searching complex networks efficiently with minimal information," Europhysics Letters, vol. 74, pp. 1102-1108, 2006.
- [14]
- CAIDA, "Toward mathematically rigorous next-generation routing protocols for realistic network topologies." Research Project. https://www.caida.org/funding/nets-nr/.
- [15]
- L. Cowen, "Compact routing with minimum stretch," Journal of Algorithms, vol. 38, no. 1, pp. 170-183, 2001.
- [16]
- M. Arias, L. Cowen, K. A. Laing, R. Rajaraman, and O. Taka, "Compact routing with name independence," in SPAA, 2003.
- [17]
- I. Abraham, C. Gavoille, D. Malkhi, N. Nisan, and M. Thorup, "Compact name-independent routing with minimum stretch," in SPAA, 2004.
- [18]
- F. Chung and L. Lu, "Connected components in random graphs with given degree sequences," Annals of Combinatorics, vol. 6, pp. 125-145, 2002.
- [19]
- W. Aiello, F. Chung, and L. Lu, "A random graph model for massive graphs," in STOC, 2000.
- [20]
- CAIDA, "Macroscopic topology AS adjacencies." https://catalog.caida.org/dataset/skitter_aslinks.
- [21]
- "The DIMES project." https://en.wikipedia.org/wiki/DIMES.
- [22]
- "University of Oregon RouteViews Project." http://www.routeviews.org/.
- [23]
- L. Kleinrock and F. Kamoun, "Hierarchical routing for large networks: Performance evaluation and optimization," Computer Networks, vol. 1, pp. 155-174, 1977.
- [24]
- C. Labovitz, G. R. Malan, and F. Jahanian, "Internet routing instability," Transactions on Networking, vol. 6, no. 5, 1998.
- [25]
- C. Labovitz, G. R. Malan, and F. Jahanian, "Origins of Internet routing instability," in INFOCOM, 1999.
- [26]
- C. Labovitz, A. Ahuja, A. Bose, and F. Jahanian, "Delayed Internet routing convergence," Transactions on Networking, vol. 9, no. 3, 2001.
- [27]
- K. Varadhan, R. Govindan, and D. Estrin, "Persistent route oscillations in inter-domain routing," Technical Report 96-631, USC/ISI, 1996.
- [28]
- T. Griffin and G. Wilfong, "An analysis of BGP convergence properties," in SIGCOMM, 1999.
- [29]
- T. Griffin and G. Wilfong, "Analysis of the MED oscillation problem in BGP," in ICNP, 2002.
- [30]
- Y. Afek, E. Gafni, and M. Ricklin, "Upper and lower bounds for routing schemes in dynamic networks," in FOCS, 1989.
- [31]
- J. M. Guiot, "A modification of Milgram's small world method," European Journal of Social Psychology, vol. 6, pp. 503-507, 1976.
- [32]
- D. J. Watts and S. H. Strogatz, "Collective dynamics of "small-world" networks," Nature, vol. 393, pp. 440-442, 1998.
- [33]
- D. Krioukov and kc claffy, "Toward compact interdomain routing." arXiv:cs.NI/0508021
- [34]
- C. Gavoille, D. Peleg, S. Pérennes, and R. Raz, "Distance labeling in graphs," Journal of Algorithms, vol. 53, no. 1, pp. 85-112, 2004.
- [35]
- P. Mahadevan, D. Krioukov, M. Fomenkov, B. Huffaker, X. Dimitropoulos, kc claffy, and A. Vahdat, "The Internet AS-level topology: Three data sources and one definitive metric," Computer Communication Review, vol. 36, no. 1, 2006.
- [36]
- B. Bollobás and O. Riordan, "Mathematical results on scale-free random graphs," in Handbook of Graphs and Networks, Berlin: Wiley-VCH, 2002.
- [37]
- F. Chung and L. Lu, "The average distance in a random graph with given expected degrees," Internet Mathematics, vol. 1, no. 1, pp. 91-114, 2003.
- [38]
- S. N. Dorogovtsev and J. F. F. Mendes, "Language as an evolving Word Web," Proceedings of the Royal Society of London B, vol. 268, pp. 2603-2606, 2001.
- [39]
- A. Berger, V. D. Pietra, and S. D. Pietra, "A maximum entropy approach to natural language processing," Computational Linguistics, vol. 22, no. 1, pp. 39-71, 1996.
- [40]
- S. D. Pietra, V. D. Pietra, and J. Lafferty, "Inducing features of random fields," Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 4, pp. 380-393, 1997.
- [41]
- P. Mahadevan, D. Krioukov, K. Fall, and A. Vahdat, "Systematic topology analysis and generation using degree correlations," in SIGCOMM, 2006.
- [42]
- J. Kleinberg, "Complex networks and decentralized search algorithms," in ICM, 2006.
- [43]
- J. Matousek, Lectures on Discrete Geometry, ch. 15, Embedding Finite Metric Spaces into Normed Spaces. New York: Springer, 2002.
- [44]
- P. Indyk and J. Matousek, Handbook of Discrete and Computational Geometry, ch. 8, Low-Distortion Embeddings of Finite Metric Spaces. Boca Raton: Chapman & Hall/CRC, 2004.
- [45]
- M. Franceschetti and R. Meester, "Navigation in small world networks: a scale-free continuum model," Journal of Applied Probability, vol. 43, no. 4, pp. 1173-1180, 2006.
- [46]
- M. E. J. Newman, "Assortative mixing in networks," Physical Review Letters, vol. 89, p. 208701, 2002.
- [47]
- M. Boguñá, R. Pastor-Satorras, A. Díaz-Guilera, and A. Arenas, "Models of social networks based on social distance attachment," Physical Review E, vol. 70, p. 056122, 2004.
- [48]
- A. Vershik, "Random metric spaces and universality," Russian Mathematical Surveys, vol. 59, no. 2, pp. 259-295, 2004.
- [49]
- B. Schweizer and A. Sklar, Probabilistic Metric Spaces. New York: North Holland, 1983.
- [50]
- P. S. Urysohn, "Sur un espace métrique universel," Les Comptes Rendus de l'Académie des Sciences, Paris, vol. 180, pp. 803-806, 1925.
- [51]
- F. Menczer, "Growing and navigating the small world Web by local content," PNAS, vol. 99, pp. 14014-14019, 2002.
- [52]
- D. J. Aldous, "A stochastic complex network model," Electronic Research Announcements of the American Mathematical Society, vol. 9, pp. 152-161, 2003.
- [53]
- D. J. Aldous, "A tractable complex network model based on the stochastic mean-field model of distance," in Complex Networks, Berlin: Springer, 2004.
- [54]
- M. Boguñá and R. Pastor-Satorras, "Class of correlated random networks with hidden variables," Physical Review E, vol. 68, p. 036112, 2003.
- [55]
- A. Fronczak, P. Fronczak, and J. A. Hoyst, "Average path length in random networks," Physical Review E, vol. 70, p. 056110, 2004.
- [56]
- J. Bourgain, "On lipschitz embedding of finite metric spaces in hilbert space," Israel Journal of Mathematics, vol. 52, pp. 46-52, 1985.
- [57]
- I. Abraham, Y. Bartal, and O. Neiman, "Advances in metric embedding theory," in STOC, 2006.
- [58]
- Y. Bartal, "Probabilistic approximation of metric spaces and its algorithmic applications," in FOCS, 1996.
- [59]
- Y. Bartal, "On approximating arbitrary metrics by tree metrics," in STOC, 1998.
- [60]
- R. Krauthgamer and J. R. Lee, "Algorithms on negatively curved spaces," in FOCS, 2006.
- [61]
- M. Thorup and U. Zwick, "Approximate distance oracles," in STOC, 2001.
- [62]
- J. Matousek, "On the distortion required for embedding finite metric spaces into normed spaces," Israel Journal of Mathematics, vol. 93, pp. 333-344, 1996.
- [63]
- J. Kleinberg, A. Slivkins, and T. Wexler, "Triangulation and embedding using small sets of beacons," in FOCS, 2004.
- [64]
- I. Abraham, Y. Bartal, T.-H. H. Chan, K. Dhamdhere, A. Gupta, J. Kleinberg, O. Neiman, and A. Slivkins, "Metric embeddings with relaxed guarantees," in FOCS, 2005.
- [65]
- A. Korman, S. Kutten, and D. Peleg, "Proof labeling schemes," in PODC, 2005.
- [66]
- A. Korman and S. Kutten, "Labeling schemes with queries." arXiv:cs.DC/0609163.
- [67]
- P. Duchon, N. Hanusse, E. Lebhar, and N. Schabanel, "Towards small world emergence," in SPAA, 2006.
- [68]
- H. Chang, S. Jamin, and W. Willinger, "Internet connectivity at the AS level: An optimization driven modeling approach," in Proceedings of MoMeTools, 2003.
- [69]
- S. Zhou and R. J. Mondragón, "Accurately modeling the Internet topology," Physical Review E, vol. 70, p. 066108, 2004.
- [70]
- S. Bar, M. Gonen, and A. Wool, "A geographic directed preferential Internet topology model," in MASCOTS, 2005.
- [71]
- H. Chang, S. Jamin, and W. Willinger, "To peer or not to peer: Modeling the evolution of the Internet's AS-level topology," in INFOCOM, 2006.
- [72]
- X. Wang and D. Loguinov, "Wealth-based evolution model for the Internet AS-level topology," in INFOCOM, 2006.
- [73]
- M. A. Serrano, M. Boguñá, and A. Díaz-Guilera, "Modeling the Internet," The European Physical Journal B, vol. 50, pp. 249-254, 2006.
- [74]
- D. Krioukov, F. Chung, kc claffy, M. Fomenkov, A. Vespignani, and W. Willinger, "The workshop on internet topology (wit) report," Computer Communication Review, vol. 37, no. 1, 2007.
- [75]
- S. Shakkottai, T. Vest, D. Krioukov, and kc claffy, "Economic evolution of the Internet AS-level ecosystem." arXiv:cs.NI/0608058
- [76]
- X. Dimitropoulos, D. Krioukov, G. Riley, and kc claffy, "Revealing the Autonomous System taxonomy: The machine learning approach," in PAM, 2006.
- [77]
- X. Dimitropoulos, D. Krioukov, M. Fomenkov, B. Huffaker, Y. Hyun, kc claffy, and G. Riley, "AS relationships: Inference and validation," Computer Communication Review, vol. 37, no. 1, 2007.
- [78]
- A.-L. Barabási and R. Albert, "Emergence of scaling in random networks," Science, vol. 286, pp. 509-512, 1999.
- [79]
- G. Manku, M. Naor, and U. Wieder, "Know thy neighbor's neighbor: The power of lookahead in randomized P2P networks," in STOC, 2004.
- [80]
- E. Lebhar and N. Schabanel, "Almost optimal decentralized routing in long-range contact networks," in ICALP, 2004.
- [81]
- C. Martel and V. Nguyen, "Analyzing Kleinberg's (and other) small-world models," in PODC, 2004.
- [82]
- P. Fraigniaud, C. Gavoille, and C. Paul, "Eclecticism shrinks even small worlds," Journal of Distributed Computing, vol. 18, no. 4, pp. 279-291, 2006.
- [83]
- L. A. Adamic, R. M. Lukose, A. R. Puniyani, and B. A. Huberman, "Search in power-law networks," Physical Review E, vol. 64, p. 46135, 2001.
- [84]
- L. A. Adamic and E. Adar, "How to search a social network," Social Networks, vol. 27, no. 3, pp. 187-203, 2005.
- [85]
- O. Cappé, E. Moulines, and T. Rydén, Inference in Hidden Markov Models. New York: Springer, 2007.
- [86]
- "The GENI initiative." http://www.geni.net/.
- [87]
- T. Roscoe, "The end of Internet architecture," in HotNets, 2006.
- [88]
- S. Farrell and V. Cahill, Delay and Disruption Tolerant Networking. Norwood, MA: Artech House, 2006.
- [89]
- P. Hui, A. Chaintreau, J. Scott, R. Gass, J. Crowcroft, and C. Diot, "Pocket switched networks and the consequences of human mobility in conference environments," in WDTN, 2005.
- [90]
- A. Chaintreau, P. Hui, J. Scott, R. Gass, J. Crowcroft, and C. Diot, "Impact of human mobility on the performance of opportunistic forwarding algorithms," in INFOCOM, 2006.
- [91]
- B. Karp and H. T. Kung, "Greedy perimeter stateless routing for wireless networks," in MobiCom, 2000.
- [92]
- A. Rao, S. Ratnasamy, C. Papadimitriou, S. Shenker, and I. Stoica, "Geographic routing without location information," in MobiCom, 2003.
- [93]
- R. Gummadi, R. Govindan, N. Kothari, B. Karp, Y.-J. Kim, and S. Shenker, "Reduced state routing in the Internet," in HotNets, 2004.
- [94]
- Y.-J. Kim, R. Govindan, B. Karp, and S. Shenker, "Geographic routing made practical," in NSDI, 2005.
- [95]
- S. Ratnasamy, P. Francis, M. Handley, R. Karp, and S. Shenker, "A scalable content-addressable network," in SIGCOMM, 2001.
- [96]
- A. Rowstron and P. Druschel, "Pastry: Scalable, distributed object location and routing for large-scale peer-to-peer systems," in Middleware, 2001.
- [97]
- P. Maymounkov and D. Mazières, "Kademlia: A peer-to-peer information system based on the XOR metric," in IPTPS, 2002.
- [98]
- D. Malkhi, M. Naor, and D. Ratajczak, "Viceroy: A scalable and dynamic emulation of the butterfly," in PODC, 2002.
- [99]
- I. Stoica, R. Morris, D. Liben-Nowell, D. R. Karger, F. Kaashoek, F. Dabek, and H. Balakrishnan, "Chord: A scalable peer-to-peer lookup protocol for Internet applications," Transactions on Networking, vol. 11, no. 1, 2003.
- [100]
- B. Y. Zhao, L. Huang, J. Stribling, S. C. Rhea, A. D. Joseph, and J. D. Kubiatowicz, "Tapestry: A resilient global-scale overlay for service deployment," IEEE Journal on Selected Areas in Communications, vol. 22, no. 1, pp. 41-53, 2004.
- [101]
- E. K. Lua, J. Crowcroft, M. Pias, R. Sharma, and S. Lim, "A survey and comparison of peer-to-peer overlay network schemes," IEEE Communications Surveys and Tutorials, vol. 7, no. 2, pp. 72-93, 2005.
- [102]
- P. Francis, S. Jamin, C. Jin, Y. Jin, D. Raz, Y. Shavitt, and L. Zhang, "IDMaps: A global Internet host distance estimation service," Transactions on Networking, vol. 9, no. 5, 2001.
- [103]
- T. S. E. Ng and H. Zhang, "Predicting Internet network distance with coordinates-based approaches," in INFOCOM, 2002.
- [104]
- Y. Shavitt and T. Tankel, "Big-bang simulation for embedding network distances in Euclidean space," Transactions on Networking, vol. 12, no. 6, 2004.
- [105]
- Y. Shavitt and T. Tankel, "On the curvature of the Internet and its usage for overlay construction and distance estimation," in INFOCOM, 2004.
- [106]
- F. Dabek, R. Cox, F. Kaashoek, and R. Morris, "Vivaldi: A decentralized network coordinate system," in SIGCOMM, 2004.
- [107]
- B. Wong, A. Slivkins, and E. G. Sirer, "Meridian: A lightweight network location service without virtual coordinates," in SIGCOMM, 2005.
- [108]
- A. Basu, A. Lin, and S. Ramanathan, "Routing using potentials: A dynamic traffic-aware routing algorithm," in SIGCOMM, 2003.
- [109]
- D. Peleg, "Proximity-preserving labeling schemes," Journal of Graph Theory, vol. 33, no. 3, pp. 167-176, 2000.
- [110]
- M. Katz, N. A. Katz, and D. Peleg, "Distance labeling schemes for well-separated graph classes," Discrete Applied Mathematics, vol. 145, pp. 384-402, 2005.
- [111]
- A. Brady and L. Cowen, "Exact distance labelings yield additive-stretch compact routing schemes," in DISC, 2006.
- [112]
- "Towards a Theory of Networked Computation." http://www.cs.yale.edu/homes/jf/ToNC.html.
- [113]
- "Internet Engineering Task Force (IETF)." http://www.ietf.org/.
- [114]
- "Internet Research Task Force (IRTF)." http://www.irtf.org/.
- [115]
- Internet Research Task Force (IRTF), "Routing research: Future domain routing scalability (RR-FS)." Working Group. https://irtf.org.
- [116]
- "Delay Tolerant Networking Research Group." https://irtf.org/concluded/dtnrg.
Footnotes:
1In reality all routing protocols used in practice support more complexity, e.g., splitting a network into areas and tracking dynamic changes intra-area while maintaining a coarser view for inter-area communication. Indeed, such hierarchical network partitioning [23] has long been considered the best approach to improving scalability.
2The delivery success ratio was later improved up to 90% [31].
3Although we cannot think of any explicit forms of information propagation in language networks [38], hidden distances still exist there and represent semantic or syntactic similarity between words [39,40].
4 having an excess of links connecting nodes with dissimilar degrees [46]
5In a different setting Manku et al. [79] showed that k-hop lookaheads (k > 1) are asymptotically as good 1-hop lookaheads.
File translated from TEX by TTH, version 3.72.
On 15 Feb 2008, 07:53.