NeTS-NR Toward Mathematically Rigorous Next-Generation Routing Protocols for Realistic Network Topologies
We propose to open a new area of research focused on applying key theoretical routing results in distributed computation to extremely practical purposes, i.e. fixing the Internet. Our agenda is ambitious, but firmly justified by a set of several previous results, all spectacularly unexpected, which have revealed a huge gap in our fundamental understanding of data networks. Our agenda has three related and clearly defined tasks: 1) execute the next step on the path toward construction of practically acceptable next-generation routing protocols based on mathematically rigorous routing algorithms; 2) validate the applicability of the above algorithms against several sources of real Internet topology data; 3) build and evaluate a model for Internet topology evolution, which reflects fundamental laws of evolution of large-scale networks.
Principal Investigators: kc claffy Dmitri Krioukov
Funding source: OAC-0434996 Period of performance: October 1, 2004 - September 30, 2008.
Project Summary
The relentless growth of the Internet has brought with it inevitable, and inextricable, economic and social dependence on this infrastructure. In reality, the dependence is mutual: without a robust source of economic support, the Internet will be unable to evolve toward the potential it quite imaginably holds. We argue that we will soon be faced with a critical architectural inflection point in the Internet, indeed for any network using the same architectural assumptions, and reaching the same size, as the Internet. Most experts agree [1,2,3,4,5,6,7,8] that the existing data network architecture is severely stressed and approaching its capability limits. The evolutionary dynamics of several critical components of the infrastructure suggest that the existing system will not scale properly to accommodate even another decade of growth. While some ad hoc patches, some of them quite clever, have offered temporary relief, the research and operational communities agree that a fundamental top-to-bottom reexamination of the data network architecture is requisite to a lasting solution. However, it remains unknown whether it is even fundamentally possible to find and support such solutions within the framework of the current data networking paradigm.
Intellectual Merit. We propose to open a new area of research focused on applying key theoretical routing results in distributed computation to extremely practical purposes, i.e. fixing the Internet. Our agenda is ambitious, but firmly justified by a set of several previous results, all spectacularly unexpected, which have revealed a huge gap in our fundamental understanding of data networks [9]. In short, we applied a recent (2001) result from theoretical computer science [10] to realistic network topologies, proving that modern routing algorithms offer dramatically superior scalability characteristics than those being used or even considered in the network research community. In concrete terms, we showed that application of [10] to the Internet topology would reduce the routing table size from an order of 100,000 (in the existing Internet) to only 50 entries. The price is a 10% increase of the average path length. Compare this tradeoff with a 15-time(!) path length increase [9] in the most ground-shaking proposals for next-generation routing [11,12] ever conceived in networking. This and other unexpected results obtained in [9] demand a radical change in our approach to research in routing, network topology and evolution. We propose here a responsive research agenda that is cohesive, well-considered, and grounded in a mathematically rigorous framework. We offer not only a strategic high-level program, but also a concrete outline of low-level practical research steps needed to pursue this agenda.
Our agenda has three related and clearly defined tasks: 1) execute the next step (following [9]) on the path toward construction of practically acceptable next-generation routing protocols based on mathematically rigorous routing algorithms; 2) validate the applicability of the above algorithms against several sources of real Internet topology data; 3) build and evaluate a model for Internet topology evolution, which reflects fundamental laws of evolution of large-scale networks.
The proposed research goals precisely match those of the NeTS-NR solicitation [13]: supporting creation of next-generation networks; increasing our fundamental understanding of large-scale complex networks; facilitating evolution of existing networks (through rigorous evaluation of their capability limits); and integrating research and education, specifically through acutely needed knowledge dissemination within and across fields.
Broader Impact. The broader impacts of this work are multi-dimensional. First, the proposed work constitutes a promising example of multi-disciplinary research, intersecting networking, theoretical computer science, and physics. Not only will the research agenda require concerted cross-fertilization across these fields, but its results will also have ramifications for research activities in all three fields. Further, the new network system modeling methodology proposed will have impact far beyond the realm of the current Internet. Indeed, the results will be elegantly generic in nature; they will dramatically increase fundamental understanding of not only the traditional Internet and data networks, but also of many other types of self-evolving large-scale systems, such as biological, social, and language networks [14].
1 Introduction
The relentless growth of the Internet has brought with it inevitable, and inextricable, economic and social dependence on this infrastructure. In reality, the dependence is mutual: without a robust source of economic support, the Internet will be unable to evolve toward the potential it quite imaginably holds. We suggest that we will soon be faced with a critical architectural inflection point in the Internet. Most experts agree [1,2,3,4,5,6,7,8] that the existing data network architecture is severely stressed and reaching its capability limits. The evolutionary dynamics of several critical components of the infrastructure suggest that the existing system will not scale properly to accommodate even another decade of growth.While some ad hoc patches, some of them quite clever, have offered temporary relief, the research and operational communities agree that a fundamental top-to-bottom reexamination of the data network architecture is requisite to a lasting solution. However, it remains unknown whether it is even fundamentally possible to find and support such solutions within the framework of present networking paradigms.
Therefore, the first high-level question we seek to answer is: will a viable next-generation data network architecture require a (by definition radical) paradigm shift? For example, will graph-theoretic abstraction of network topology eventually be insufficient? To answer this provocative question, we must find mathematically rigorous bounds for scalability-related parameters e.g., routing table size and path length inflation, of an architecture based on the current graph-theoretic paradigm. The lower bounds are of particular theoretical interest for us since they imply that a given scalability parameter in any potential solution cannot grow slower than its lower bound. Thus, if the theoretical lower bounds, which indicate how well a system can scale in principle, are high, then a paradigm shift is inevitable. We might conclude, for example, that a graph-theoretic representation of network topology carries inherently, and dramatically, poorer scaling characteristics than alternative approaches.
On the other hand, if the theoretical analysis yields practically acceptable results, then the next question is: can we find any algorithms whose upper bounds approach the theoretical lower bounds? If such algorithms exist, we must determine next if they can be implemented as protocols that would satisfy other practical requirements [6], and if they can be seamlessly deployed in a next-generation network architecture. This process constitutes our high level research agenda.
The component of the present data network architecture that suffers, and faces, the most stress is arguably the routing system [1,2,3,4,5,6,7,8]. While the data plane can support forwarding lookups on tables of up to millions of entries [15], empirical observations have shown that the control plane is already close to its capability limits [8]. The problem is not routing table size per se, but the relationship between increasing table sizes and routing convergence times. Further, the challenge has two dimensions [2]: first, can routing hardware scale appropriately; and second and more fundamental, are optimal routing convergence times and routing stability even achievable in principle, regardless of hardware limitations.
We also note that routing scalability parameters depend strongly on characteristics of the underlying network topology. Not only network size, but also its structure, matters. One intuitively expects that routing on a `nice clean topology' is easier than on a random dynamic `mess'. Therefore, we care about realistic topologies, and since our concern is scalability, we must consider real, large-scale networks. Note that accurate knowledge of network topology is essential not only to routing, but also to other networking functionality, ranging from traffic measurement and characterization to economic and even social aspects of communication networks. Heightened interest in national cybersecurity has highlighted the analysis of network resilience to both random failures and hostile attacks [14] as a critical priority requiring precise topology knowledge.
We address our questions at the highest level of abstraction possible within present networking paradigms-scalable routing on idealized graphs. Staying general as long as possible will allow us to obtain rigorous results (outlined in Section 4.1) applicable to many types of networks, including overlay as well as programmable wireless and sensor networks. That said, we recognize that the Internet, the largest data network known, is an ideal and obvious domain for investigation of scalability questions. Indeed, the most severe routing scalability problems widely known today have occurred in Internet interdomain routing [1,2,3,4,5,6,7,8]. So while the impact of the proposed work transcends the current Internet architecture, the research will require that we increase and disseminate our knowledge about the true topology of the Internet (see Section 4.2).
Another question we must answer in order to ensure long-term practical value of our theoretical results: what are the fundamental laws of network evolution? If we gain deep insight into existing network topology, but develop no model that can predict how it will evolve, the relevance of our results is fleeting. This concern is well-founded, given that the current Internet routing architecture is rooted in an assumption that is no longer valid: a sparse topology allowing for hierarchical network partitioning [16]. This assumption was true during the early days of the ARPANET [17] but no longer holds today [7], and we argue that this conflict is a fundamental cause of observed scalability issues [9]. We thus propose to build and evaluate a model for Internet topology evolution, one that reflects fundamental laws of evolution of large-scale networks and also explains our revelations in [9]. Discerning the true forces driving evolution of large-scale networks offers not only predictive power in the face of exogenous changes to the system, but also potential knobs of influence.
In summary, our focus is on next-generation routing proven to scale well into the future evolution of real network topologies.
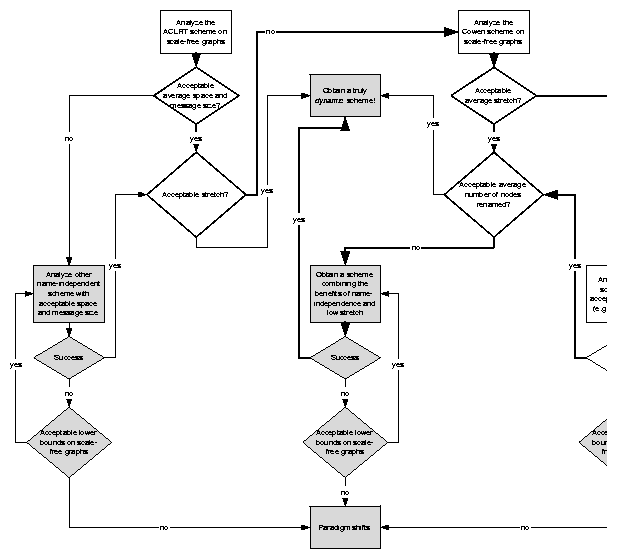
We structure the proposal as follows. We first provide, in Section 2, some background on Internet routing, topology, and evolution to set up context for our research agenda. We then give a detailed rationale for why we argue that a radical shift in emphasis is necessary, which includes explaining the spectacularly surprising results that inspire our proposed agenda (Section 3). In Section 4 we describe our proposed research agenda, which involves three related tasks: in routing, topology, and modeling Internet evolution. Figure 2 is a logistical flowchart of our routing research agenda.
2 Background
2.1 Routing Theory
A mathematically rigorous formulation of scalability aspects of routing in networks is a well-studied problem in the theory of distributed computation [18]. At the core of this problem is a triangle of trade-offs among routing table size, convergence parameters, and path length inflation. By ``trade-off'' we mean that, for example, routing table size decrease comes at a price of increase in average path length.
In distributed computing, the routing table size is usually referred to as the memory space, meaning the amount of memory required by a routing algorithm either per node (called local space) or for the whole network (the total memory space). We will also call a routing algorithm a scheme [19], but we will differentiate between a scheme and a routing protocol, an implementation of a given routing scheme that can be deployed in real networks.
The convergence parameters, which we will collectively call adaptation costs [20], can be, for instance, the (maximal) number of control messages generated by a routing scheme per topology change, or sizes of those messages.1 For example, according to theoretical work in [21,22] as well as experimental observations [23,24], we know that adaptation costs of the existing Internet routing architecture have an infinite upper bound since there are scenarios where the Internet interdomain routing protocol (Border Gateway Protocol-BGP) does not converge at all!
Finally, the path length inflation is measured by stretch. The stretch is a worst-case multiplicative path length increase factor associated with a given routing scheme. For example, a stretch-3 routing scheme produces paths that are at most three times longer than the corresponding shortest paths. Stretch-1 routing and shortest path routing are synonymous.
In the existing routing architecture, high memory space and adaptation costs are practical scalability problems. Since almost all currently deployed routing protocols are based on a small set of shortest-path routing algorithms, stretch is not a practical concern. However, stretch might easily become relevant if we consider non-shortest path (stretch > 1) routing algorithms.
The memory space, stretch, and adaptation costs of a given routing scheme depend strongly on the topology of the network to which the routing scheme is applied. In other words, the topological properties of real networks transform the theoretical parameters outlined above into the real scalability problems the Internet faces today [25]. Therefore, any rigorous routing research capable of producing practically viable results depends on validation against real topology data, which requires maintaining accurate sources of such data.
2.2 Internet Topology
For the reasons mentioned in the Introduction, the real network of most interest is the Internet. Many parameters characterizing Internet topology have power-law distributions [26,27]. Although the question of how closely the real Internet topology follows power laws remains open to debate [28,29,30,31], the fact that Internet topology at the granularity of Autonomous Systems (ASs) is a fat-tailed scale-free small-world [26,27,7,32,14] network is not in dispute.
Both the fat-tail and scale-free properties refer to node degree distribution in a graph, but often overlooked is the fact that these two topology characteristics are completely independent [14]:
- The node degree distribution has a fat tail if there is a noticeable number of high-degree nodes (``hubs'') in the graph.
- The graph node degree distribution is scale-free if it lacks any characteristic scale, which effectively means that the graph has many low-degree nodes.
Graphs with power-law node degree distributions possess both properties, as opposed to classical Erdös-Rény random graphs [33], where any pair of nodes is connected with a fixed probability. Node degree distributions in such random graphs are close to a narrow Poisson distribution centered around its average (characteristic scale) and exponentially decreasing at high degrees. The term scale-free is often used as a substitute for power-laws, and we adhere to this terminology in this proposal.
Scale-free networks necessarily possess the ``small-world'' property [34,35,36]. Indeed, even a moderate number of `hubs' guarantees low average shortest path length (or simply the average distance) and low width of the distance distribution [34]. In other words, in small-world graphs, the first two moments of the distance distribution are small.2 For example, in the AS-level graph of the Internet, the average AS-hop distance is approximately 3.5 and the dispersion is around 1 [7,32]. Approximately 86% of AS pairs are at a distance of 3 or 4 AS hops.
The small-world property and other properties of scale-free networks are intricate [14] and drastically affect traditional views, approaches, and even methodology of network-related research [30]. Unfortunately, in many cases (including the Internet case) other graph classes with quite different properties have been traditionally assumed to be sufficiently accurate models for realistic networks. We now know that these models have little to do with reality [38], a gap that demands fundamental reexamination of what we know about large-scale networks, and in particular what depends on their topology. This proposal represents an initial itinerary for this process.
2.3 Internet Evolution
The first step of such reexamination is to provide a rigorous explanation of evolutionary dynamics responsible for the appearance of power laws in the Internet. Beyond its immediate practical importance to routing research, this question has two other fundamental aspects with long-term value (cf. Section 1):
- The Internet is one of many examples of scale-free networks [14], and it is possible that its laws of evolution may derive from more general laws of network evolution.
- Empirical discovery of power-laws in many networks came as a big surprise-there had been virtually no theoretical prediction that power-laws would hold in such a large number of different types of networks. Indeed, most believed that the Internet in particular possessed quite different structures and properties [38]. This observation implies that a fundamental piece of understanding of large-scale networks was missing.
The above two considerations have inspired great recent popularity in the field of network evolution modeling. Since the discovery of power laws in the Internet [26], the number of proposed models has grown rapidly, including from both networking [39,40,41,42] and statistical physics [43,44,45,46,47,48,49,50,51,52,53,14] (studying the dynamics of complex systems at the fundamental level). However, there is arguably not yet any Internet evolution model that is satisfying from both networking and physical standpoints [25]. As a consequence, the fundamental laws governing Internet evolution remain unclear. The central obstacle on the path toward a satisfying model is the methodological barrier described below.
On one hand, the Barabási-Albert (BA) preferential attachment model [43] and its derivatives [44], popular among physicists, have received much criticism from the networking community [30,31] for being too general, not incorporating domain specifics, and hence failing to accurately predict many peculiarities of Internet topology and evolution.
On the other hand, the only explanatory [30] model proposed by the networking community [41] tries to incorporate Internet evolution specifics by introducing a number of external parameters that allow one to easily fit the output of a model to observed data. The proliferation of parameters is not comforting, since any model with a sufficient number of external parameters can be forced to produce any required output by parameter manipulation.
A system model represents the fundamental laws of evolution laws when all its parameters can be expressed via physical variables [14] or when the physical values of the external parameters (such values correspond, for example, to properly defined analogs of the minimum energy or maximum entropy in the system) match the observed data. In other words, a model reflecting the fundamental laws of the system dynamics should reproduce observed data with a minimum number of external parameters obtained via data fitting procedures. There is currently no such Internet evolution model. We propose to build one.
3 High-Level Rationale
3.1 Routing in the Internet
The direct causes of Internet routing table growth are well-studied: increasing topology density, including multihoming and peering; routing policies; inbound traffic engineering; address allocation policies; etc. [54,7,3,4] Several efforts, proposals, and even new routing architectures seek to address those factors. Prominent efforts in this direction are, for example, the Beyond BGP [55] and Atomized Routing [56] projects, the ISLAY routing architecture [12], the activity of the MULTI6 working group [57], etc. However, we argue that even if we could manage to deploy any of the proposed approaches, it would only represent another short-term patch, because they address not the root of the problem but its symptoms. The Internet needs more than a short-term solution.
Consider the ISLAY architecture, which implements the idea of routing on AS numbers: AS numbers (or aggregate identifiers, in the terminology of [12]) become addresses within an interdomain routing protocol. This approach would immediately reduce the routing table size by an order of magnitude (there are an order of 105 of IP prefixes in the global routing table today and an order of 104 ASs). However, over time, an increasing number of small (stub) networks will want to participate in interdomain routing, e.g., for traffic engineering reasons, and would require their own AS numbers. Such small networks would utilize tiny portions of the public IP address space, and the total number of ASs would grow to the same order as the total number of IP prefixes, and we will end up facing essentially the same problem we have today. Lending further credibility to this hypothesis is the empirical observation in [7] that even in the existing Internet, the number of ASs na grows faster than the number of IP prefixes np: np ~ na2/3.
This example demonstrates the need to investigate the problems at their most fundamental level in order to find sustainable scalable solutions. We argue that any sustainable long term solution must rely on routing algorithms with practically acceptable rigorous bounds for memory space, stretch, and adaptation costs on graphs with realistic topologies.
We contend that the most sophisticated concept about routing scalability that the networking community is aware of seems to be aggregation, i.e. multiple levels of hierarchical network partitioning in the manner of the Kleinrock-Kamoun (KK) routing scheme [16], which introduced the idea of hierarchical routing and analyzed the trade-off between memory space and stretch for the first time.
Unfortunately, the KK scheme did not provide any algorithm for construction of the required network partitioning, i.e., the hierarchy itself. Furthermore, assuming that a required partitioning exists, Kleinrock and Kamoun showed that the stretch produced by their scheme would be reasonably low only for sparsely connected networks with high average path lengths [16]. Today we know that the Internet, being a scale-free network, bears the small-world property (cf. Section 2.2), which means that its average path length is small. As we analytically showed in [9], the stretch produced by the KK scheme on the real Internet topology would be extremely high-15, meaning routing could produce paths as much as 15 times longer than the shortest path between the same two points. This result has a radical implication: proposed routing architectures based on hierarchical network partitioning (Nimrod [11], ISLAY [12], etc.) are not realistic.
Fortunately, the theory of distributed computations has accumulated a significant number of impressive results in the routing area. Several recent compact routing schemes [58,10,59] guarantee succinct routing tables but with much smaller increase of stretch than in the KK case. Note that we must allow the stretch to increase since generic (i.e., applicable to all graphs) shortest path routing is incompressible [60]. More precisely, the memory space lower bound for generic shortest path routing is as high as the upper bound of trivial shortest-path routing O(n logn), where n is the network size.
However, shortest-path routing is an essential requirement for any realistic interdomain routing. For example, a routing scheme that would prevent a pair of adjacent ASs from utilizing a shortest-path peering link between them would be operationally unacceptable. Thus, any stretch > 1 routing scheme applied to the Internet for operational use will require some augmentation of the routing tables with shortest-path routing information. Such increase of memory space might break the theoretical memory space upper bound of the routing scheme.
Thus, the first applicability concern regarding modern compact routing schemes is how far their average stretch on realistic scale-free graphs is from 1. In other words, the specific first question on the path toward a scalable next-generation routing architecture is: is it possible to construct a routing scheme simultaneously characterized by low memory space and low stretch on realistic scale-free network topologies? We answered this question positively in [9].
3.2 Our Previous Work
|
In 2003 we found that one of the three pairs of trade-offs discussed in Section 2.1, namely, the memory-stretch trade-off, is surprisingly good on realistic scale-free topologies [9]. We considered the recent static stretch-3 routing scheme by Thorup and Zwick (the TZ scheme) [10]. The stretch value of 3 is the minimal stretch value allowing for significant reduction of the local memory space lower bound [19,61]. The TZ scheme is the only known nearly optimal stretch-3 scheme. Its local memory space upper bound of O(n1/2log1/2n) is nearly (up to a logarithmic factor) equal to the theoretical lower bound of W(n1/2) [62].
Using methods of probability theory and mathematical analysis, we derived the approximate analytic expression for the average stretch produced by the TZ scheme on any graph. This expression turned out to be a function of only the first two moments of the distance distribution in a graph.
We also implemented the TZ routing scheme so that we could simulate its performance on Internet-like graphs produced by the power-law random graph (PLRG) generator [63].3 We obtained a close match between analysis and simulations and found that both the routing table size and stretch produced by the TZ scheme are small on Internet-like topologies. For 104-node graphs, the routing table size had only 52 entries, and the stretch was around 1.1 [9]. This result proves that for realistic scale-free graphs, there is no fundamental conflict between memory space and stretch. This first step points to a well-defined path toward future work in this area, as we describe below in Section 4.1.
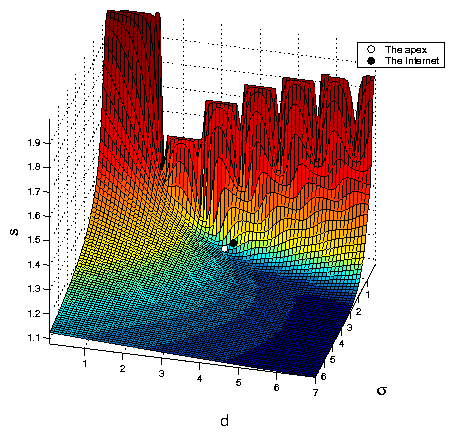
In the same study we discovered something of even greater theoretical importance: the Internet's proximity to the unique critical point of the TZ stretch function. Our analytical results allowed us to collect sufficient numerical data to analyze in detail the structure of the average stretch function. We showed that this structure has a unique point (called the apex) characterized by a set of critical phenomena [9]. What astonished us was how nearby this apex was the point most closely representing the real Internet topology, according to the best topology data sources available (see Figure 1).
This finding is absolutely unexpected, and points to a huge gap in our fundamental understanding of the Internet. Specifically, no one has ever assumed that laws of Internet evolution had anything to do with stretch. Our discovered connection demands a concerted search for relationships between the memory-stretch trade-off and laws of Internet evolution (cf. Section 4.3).
4 Proposed Research Agenda
We are now prepared to describe in detail our proposed research program. Our agenda has three related and clearly defined tasks: 1) execute the next step (following [9]) on the path toward construction of practically acceptable next-generation routing protocols based on mathematically rigorous routing algorithms; 2) validate the applicability of the above algorithms against several sources of real Internet topology data-this tasks requires that we also quantify and compare the precision of these data sources, which has been needed by the Internet research community for several years; 3) build and evaluate a model for Internet topology evolution, which reflects fundamental laws of evolution of large-scale networks and which explains our revelations in [9]. We describe each task in detail below.
4.1 Compact Routing
Methodology. We propose to apply the methodology we used in [9] (cf. Section 3.2) to several routing schemes proposed in the recent literature [64,58]. We will focus on the stretch-5 scheme obtained in [64], which we will call the ACLRT scheme for the author names, and on the scheme from [58], the Cowen scheme. We will first seek analytic solutions for the average memory space, stretch, and other relevant performance characteristics of these schemes on realistic topologies. We will also implement the schemes for simulation purposes, extending the software we wrote to simulate the TZ scheme in [9]. We will generate random graphs with specified realistic topologies and analyze distributions of each scheme's performance characteristics on generated graphs. Figure 2 shows a logistical flowchart of our routing research program.
4.1.1 Toward Dynamic Routing: Name Independence
We will analyze the average performance parameters (local memory space, stretch, control message sizes, etc.) of the ACLRT scheme [64] on realistic network topologies. The ultimate goal of this work is either: 1) to find a dynamic routing scheme with practically acceptable upper bounds for the above parameters on scale-free graphs; or, 2) to find unacceptable lower bounds demonstrating that such routing is impossible in principle.
Rationale. While we showed that both the memory space and stretch can be made extremely small on scale-free graphs, we assumed unbounded adaptation costs in [9]. In other words, we considered the static case, whereas any realistic routing protocol must be dynamic.
The mathematically rigorous approach to routing on dynamic graphs is fundamentally hard. The question of whether it is possible, in principle, to efficiently represent a highly dynamic object, a real network, by an intrinsically static construct, a graph, seems to be at the root of the difficulty [65]. Increasing the perceived challenge is our knowledge of several pessimistic lower bounds. For example, assuming unbounded memory space and message size, there is always an n-node graph such that any generic stretch-s routing scheme has to produce an order of n/s control packets to converge after some topology change on this graph. In other words, the adaptation cost lower bound is W(n/s) [66]. The implication of this lower bound is, for example, that if we consider shortest path routing on all graphs of size n, then we cannot guarantee less than an order of n routing control packets per topology change, which is practically unacceptable.
However, we saw in [9] how surprisingly good the scale-free graphs turned out to be with respect to the memory-stretch trade-off, which is much worse in the generic case [19]. Therefore we might expect that if we narrow the class of graphs to the scale-free graphs, the dynamic case trade-offs would also improve significantly.
The first practical step to verify the above conjecture is to analyze name-independent routing schemes. The scheme we considered in [9] is not name-independent; it renames network nodes to encode useful topological information in their names. As soon as any node or link failure occurs, the topology changes, and there are no bounds for the amount of nodes that need to be renamed as a result of topology change.
Fortunately, the authors of [64] have recently made significant progress in construction of low-stretch name-independent compact routing schemes. For example, they obtained a name-independent stretch-5 scheme (the ACLRT scheme) with local memory space upper bound of [O\tilde](n1/2)4 and message header size upper bound of O(log2n). Our first routing research goal is to analyze the behavior of name-independent routing schemes on realistic network topologies.
Importance. Either a positive or negative outcome of this research task is important. If we find the scheme's performance practically acceptable (including the required behavior of the average stretch as a function of n, cf. Section 4.1.2 below), then the next step in routing research is to develop a truly dynamic scheme based on ACLRT. However, a negative result implies that we must pursue more fundamental analysis of lower bounds for name-independent routing on scale-free graphs. See Figure 2 for a logistical flowchart of our routing research program.
4.1.2 Shortest Path Routing
|
We will first consider the average stretch as a function of n for the ACLRT scheme (cf. Section 4.1.1. If we find that the average stretch does not approach 1 fast enough in the limit of large n (see below), then we will apply our methodology to analyze the average stretch of the Cowen scheme [58] on realistic network topologies. The ultimate goal of this task is either: 1) to find a routing scheme with a practically acceptable upper bound for the number of non-shortest paths on scale-free graphs; or, 2) to find an unacceptable lower bound demonstrating that such a routing scheme does not exist.
Rationale. In [9], we found that the average TZ stretch [`s](n) on scale-free graphs, being a decreasing function of the network size n, does not approach 1 in the limit of infinite n. Therefore, the upper bound for the average number of non-shortest paths per node nlp(n) is O(n) since nlp(n)=([`s](n)-1)n. As discussed in Section 3, shortest path routing is a strict requirement for practical usability of a routing scheme. Therefore, if a maximum stretch > 1 routing algorithm is used in real networks, then some portion of (or all) non-shortest paths produced by such scheme must be algorithmically replaced with shortest paths, which will increase the local memory space upper bound. Thus, if the TZ scheme is used in practice, then its routing table size upper bound will increase back from [O\tilde](n1/2) to the limit of incompressible shortest path routing O(n).
In other words, if we want the stretch-3 local memory upper bound to stay at [O\tilde](n1/2), then the number of non-shortest paths must also have the same upper bound. Using the relation between the average stretch [`s](n) and the average number of non-shortest paths per node nlp(n), [`s](n)=1+nlp(n)/n, we conclude that [`s](n), in the limit of large n, must approach 1 not slower than 1+n-1/2+o(n-1/2).
The above considerations suggest that we should analyze the schemes with lower (than in the TZ case) average stretch values on scale-free graphs. In [25] we argued that the Cowen scheme [58] should produce such lower values. This task will target analysis of this scheme, and possibly other schemes from [59] (EGP schemes) and stretch-(2k-1) schemes from [10] (TZH schemes, Thorup and Zwick Handshaking).
Importance. Yet again, either a positive or negative outcome of this research is critically important. If we find that the average stretch is small enough for a scheme other than the ACLRT scheme in Section 4.1.1 (e.g. the Cowen scheme), then the next step in routing research is to construct a name-independent routing scheme preserving the newly discovered small average stretch. However, if we do not find any routing scheme with the required asymptotic behavior of the average stretch function, then we must pursue more fundamental analysis of lower bounds for the number of non-shortest paths on scale-free graphs.
4.2 Validating Against Internet Topology
Accurate measurements and analysis of network topology are critical for routing research since performance trade-offs associated with a given routing scheme are functions of the network topologies to which the routing scheme is applied. If we show that a routing scheme has satisfactory performance characteristics for a given class of topologies, but the real network topology turns out to be different, and in particular lowering the performance of the routing scheme, then our findings will have only theoretical value and no practical use.
Ideally, we seek a routing scheme designed specifically for real-network topologies, indeed one that can efficiently handle topological peculiarities. While there are many routing schemes constructed for regular graph classes the graph theory has traditionally liked to deal with [19], there is none for scale-free graphs. The conspicuous gap in rigorous graph-theoretic results on properties of scale-free graphs [67], partially attributable to the complexity and novelty of the subject, inhibits progress in this direction. Therefore, we must retreat to analysis of generic, i.e., applicable to all graphs, routing schemes on realistic topologies (cf. Section 4.1), but for this analysis to be of practical use, we must know exactly what those realistic topologies are.
Fortunately, CAIDA has established itself as the richest source of macroscopic Internet topology data available anywhere, and has sustained unprecedented granularity in Internet topology measurement coverage for over five years. We are ideally positioned to validate the results of our routing research against existing and future massive empirical Internet topology data sets [68,69,70,71]. The topology component of our agenda is two-fold: (1) continue to make available to the research community the most comprehensive and accurate source of Internet topology data; and (2) quantifying and comparing the precision of different topology sources currently being used by the research community.
4.2.1 Traceroute-Based AS-Level Topologies
To facilitate community access to Internet topology data, we will make traceroute-derived AS adjacency matrices available from our website [72]. We will be posting these snapshots of Internet AS-level graph daily, as well as archiving historical data.
Methodology. Under the Macroscopic Topology Project [73], CAIDA has already developed the significant infrastructure for continual traceroute-based Internet topology measurements. We will extend current CAIDA software to automatically map these measurements into AS adjacency matrices representing the Internet graph at the AS level.
Rationale. The rationale for this task is to provide an easier community access to more accurate and complete Internet topology data.
Many key publications of Internet topology analysis and modeling [26,38,31,41,44,14] have relied on NLANR/RouteViews [74,75] BGP data. However, several researchers have independently shown that BGP-based topology measurements yield results that are different [76,77] from those based on traceroute-based measurements [68]. Network topologies derived from traceroute measurements are more likely to reflect the topology of actual traffic flows than BGP data.
Importance. The results of this work will have broad impact not only on the networking but also on physical science communities, who are actively using results of Internet topology measurements [26,27,39,38,31,30,41,44,40,32,45,48,49,50,51,52,53,14]. A user-friendly interface to gathered Internet topology data will facilitate severely needed dissemination of this critical knowledge to the research and operational communities.
4.2.2 Comparative Analysis of Internet Topologies
We will compare the Internet AS-level topologies derived from WHOIS- [78], BGP- [75], and traceroute-based data [68,69]. The goal is two-fold: 1) to quantify the precision of different topology data sources; and, 2) to derive a definitive set of network topology characteristics for topology comparisons.
Methodology. We will obtain the traceroute-based topology views in Section 4.2.1 above. To obtain a BGP-based topology, we will use existing tools (e.g., rv2atoms [79], developed as a part of CAIDA's Atomized Routing Project [56], to map RouteViews [75] data to AS adjacency matrices. Using tools from [80], we will also parse the WHOIS database for the same purpose.
For each topology view, we will calculate the critical set of the most important topology characteristics. This set will include the network size (number of nodes), number of links, node degree distribution, distance distribution, betweenness,5 correlation parameters (clustering coefficients, node degree correlations, numbers of cycles of different lengths, graph spectrum, etc.) and other graph-theoretic characteristics. We will also define and evaluate, on all the three classes of Internet topology view described above, a characteristic measuring the description complexity of the graph adjacency matrix in the spirit of Kolmogorov theory [82,83]. We will call this parameter the graph entropy, which is different from the better-known definition of the graph entropy given in [84].6 We realize we will not be able to consider all possible graphs characteristics in our analysis. We will focus on those characteristics most frequently used in network evolution modeling [42,40,41,43,45,32,44,14] and in comparison of networks topology generators [39,38].
Rationale. An increasing number of network evolution models and topology generators use inaccurate or incomplete topology data sources for validation purposes (see above for references). This situation renders it even more important to quantify the differences between Internet topology views obtained from different data sources.
Importance. A logical continuation of our earlier work analyzing incongruity between different sources of topology data [76], this task will provide a source of quantifiable information on the precision of available Internet topology data sources. The result will have significant educational impact on the community-specifically, it should inhibit over-enthusiastic researchers from suggesting weakly supported but far-reaching conclusions about Internet topology and its evolution.
This work will also help to distill a minimal set of the most important network topology characteristics that should be used to compare topologies, e.g., those produced by topology generators versus real network topologies.
4.3 Modeling Internet Evolution
We will build and evaluate an economy-based model for Internet topology evolution. Our primary goal is to increase our fundamental understanding of the laws of evolution of large-scale networks.
Methodology. The economic realities of the ISP business are the primary drivers of evolution of Internet topology at the AS level [86]. We will encode these realities in our model in the following way.
Our model will operate on the AS-level graph directed according to inferred customer-provider relationships [87]. Every new (customer) node will connect to an already existing node (its provider) according to our modification of the heuristically optimized trade-off (HOT) algorithm introduced in [88]. We will model geographic distance similarly to [88]. The provider preference (its weight) will be proportional to the number of the network destinations the provider can reach for free, i.e. via its customers, peers, and peers' customers. One of the main drivers for multihoming is higher reliability of network connectivity. We will model this driver by an exponentially decreasing probability to connect to one more provider. The main incentive for peering is to decrease transit costs. In our model, peering between providers will occur when the providers are geographically close and mutually attractive-namely, when there is a similar count of additional free network destinations acquired by each provider via peering. Including peering naturally into the model represents a step forward relative to [41].
The above construction will introduce a number of external parameters into the model. We will find the parameter values that match (based on the set of topology characteristics described in Section 4.2.2) observed Internet topology data (Section 4.2.1). Note that this data will not contain the semantics of customer-provider relationships that we require for our topology comparisons. However, we will add this necessary component to the data using results from our AS Ranking project [70].
After matching the observed data by manipulation of external parameters, the usual network modeling methodology (as well as complex system modeling methodology in general) ends with simulating various ``what-if'' scenarios within the obtained model. As we argued in Section 2.3, this approach is of certain practical use but of no theoretical value since there is an infinite number of models capable of reproducing the same observed data and there has been no methodological consideration to prefer one such model to another. We will extend the traditional methodology as follows.
Holding all other parameters fixed, we will vary each parameter in the model, measure the entropy of the resulting graphs, and determine if the parameter value matching the observed data is close to the value that maximizes resulting graph entropy. This technique allows us to filter out parameters that do not reflect fundamental laws of Internet evolution. Indeed, if the maximum entropy and data-matching values of a parameter are equal, then such a parameter represents a system component that has evolved to its maximally random state since according to our definition of graph entropy (cf. Section 4.2.2), higher-entropy graphs are ``more random''. However, if the opposite is true, the component represented by the parameter is not free; instead it is fixed by an external constraint, which is an actual law driving the system evolution. Note that this technique is an application of the maximum entropy principle [89,90] for a system subjected to set of external constraints, which represent its evolution laws.
By its construction, our model will be explanatory in the terminology of [30]. At the same time, we observe that the recent evocative [30] model introduced in [42] closely reproduces the most important Internet topology characteristics.7 Therefore, while we do not expect our model to be analytically solvable, we will compare topologies produced by the two models and will check if the preferential attachment function considered in [42] can be derived from within our model.
If it can, it effectively demonstrates that a BA-based approach with a specific form of preferential attachment function (considered in [42]) yields essentially the same result as our explanatory model. That is, we will demonstrate the presence of a link between the explanatory and evocative network evolution model classes discussed in [30].
Rationale. There are several motivations for this modeling task:
- Traditional arguments for network evolution modeling apply. Specifically, we can use this model as a topology generator, as well as a simulation environment for various realistic ``what-if'' scenarios, e.g. How will Internet topology look if ISP business realities change in a certain way?, or Can we influence the Internet economy so that it would result in a more desirable Internet topology?
- The next-generation network research community desperately needs sound methodologies for evaluating a wide class of formal models that attempt to not only faithfully reproduce observed data, but also capture fundamental laws of network evolution (cf. Section 2.3). The extended methodology we propose to utilize is the first step in this direction.
- Closely related to the above is the current lack of explanation of the Internet's proximity to the stretch apex (cf. Section 3.2). The model we propose to investigate will help us discover the explanation. Indeed, since stretch is a natural measure of system performance, and the memory space is directly related to the graph entropy [82,83,19], then a network evolution model having entropy-performance trade-offs embedded in its core might be capable of explaining the effects in [9]. As was observed in [88], the trade-offs in question are closely related to the HOT trade-offs we will build into our model.
Importance. The extension of network modeling methodology proposed in this section will have impact beyond the realm of the current Internet. Indeed, the results will be elegantly generic in nature; they will shed light on evolution of not only the Internet but also of many other types of self-evolving large-scale networks, such as biological, social, and language networks [14].
5 Conclusion
The current circumstances in the fields of theoretical computer science (TCS) and networking have created a rare opportunity to pursue a fundamental breakthrough in a vitally important area: scalable routing on real world networks. Our application of a recent result in TCS to Internet-like graphs yielded a shockingly promising result: we may have found an alternative routing scheme that offers dramatically superior scalability characteristics, i.e., routing table size and path length inflation, than those being used or even considered in the field of networking. Faced with these discoveries, we recognize a need for radical change in our approach to routing research, network topology and evolution, in order to integrate, and build on, outstanding modern results from theoretical computer science. In particular, we need to determine how applicable these results are to highly dynamic real world networks. We propose here a responsive research agenda that is cohesive, well-considered, and grounded in a mathematically rigorous framework. We offer not only a strategic high-level program, but also a concrete outline of low-level practical research steps needed to pursue this agenda. An emphasis of our work will be validating results against data from the current Internet, which has evolved, through a series of phase transitions, from a small research network designed and fully controlled by a group of few enthusiasts [91] into a huge network interconnecting thousands of independent and even adversarial networks, with no point of external control. Construction of realistic, efficient, and scalable routing for the next-generation Internet is a key motivator of our work. But the better news is that our proposed work will not only advance our understanding of the Internet, but also contribute significantly to understanding fundamental laws governing the evolution of many large-scale complex systems, of which the Internet is only one example, albeit of critical strategic interest.
6 Work Plan
Year 1: 1) analyze the ACLRT scheme (see Section 4.1.1 and Figure 2); 2) start posting AS-level adjacency matrices of traceroute-derived Internet topology graphs (see Section 4.2.1).
Year 2: 1) analyze the Cowen scheme (see Section 4.1.2 and Figure 2); collect the topology data from different data sources and compare the observed topologies with regard to characteristics listed in Section 4.2.2; 2) provide detailed specification and implementation (simulation of) the Internet evolution model from Section 4.3.
Year 3: 1) analyze the EGP and TZH schemes (see Section 4.1.2 and Figure 2)-we may need to apply our analysis to some future routing schemes that are superior to the proposed schemes, we will judge their superiority according to the arguments discussed in Section 4.1; 2) compare topologies produced by Internet topology models and Internet topology generators with real Internet topologies, which will require constructing an extended set of characteristics over which network topologies should be analytically compared (see Section 4.2.2); 3) apply the extended network evolution modeling to our economy-based Internet evolution model as well as to other models (see Section 4.3).
7 Broader Impact: Outreach to the Community
Dissemination of knowledge. The proposed research agenda is multi-disciplinary. It intersects networking, theoretical computer science, and physics, and inherently involves increased flow of knowledge among these fields. In addition to publishing our results via conferences and journals, we will present our results to network engineering and operational communities at the IETF [92] and NANOG [93] meetings.
One of the PIs, Dr. Krioukov, is the chair of the IRTF [94] Routing Research [95] Future Domain Routing Scalability Working Group [96] chartered with an agenda related to work proposed here. His responsibilities as a chair include providing, at the IETF meetings, yearly reports on the status of research covered by the working group charter [96]. The other PI, Dr. Claffy, is a member of the NANOG program committee which promotes the presentation of research topics that are of compelling operational relevance to providers and vendors. NANOG meetings occur three times per year.
Each year of the project, CAIDA will also host a workshop to bring together the research and educational communities to summarize efforts from the previous year, stimulate new research ideas, and revisit priorities for the next steps. These workshops will be in our Internet Statistics and Metrics Analysis (ISMA) workshop series [97]. They will focus on different research topics each year.
Dissemination of data. The main goal of the task in Section 4.2.1 is to provide the community with an easy access to accurate Internet topology data. We will be posting daily updates of the AS-level adjacency matrices of the Internet graph on our website [72].
Research and education. The research, analysis, and measurement work at CAIDA offers a rich opportunity for students to gain experience in operationally relevant Internet research. This grant will allow us to host two graduate students for nine months for each year of the grant, and one graduate student for a full year. CAIDA often hires students from institutions other than UCSD; during the summer of 2004 we will host a student from Dr. Lixia Zhang's `Beyond BGP' (NSF-funded) project [55], fostering cross-fertilization with that project.
8 Results from Prior NSF Support
``CAIDA: Cooperative Association for Internet Data Analysis.'' ANI-9711092. $3,143,580. Oct 1997 - Jul 2001. (Claffy) This collaborative undertaking brings together organizations in the commercial, government, and research sectors. CAIDA provides a neutral framework to support cooperative technical endeavors, and encourages the creation and dissemination of Internet traffic metrics and measurement methodologies [98]. Results of this collaborative research and analytic environment can be seen on published web pages on the CAIDA web site www.caida.org. CAIDA also develops advanced Internet measurement and visualization tools.
``Internet Atlas.'' ANI-99-96248 $304,816. Jan 1999 - Dec 2001. (Claffy) This effort involves developing techniques and tools for mapping the Internet, focusing on Internet topology, performance, workload, and routing data. A gallery that assesses state-of-the-art in this nascent sector is published on the web [99].
``Correlating Heterogeneous Measurement Data to Achieve System-Level Analysis of Internet Traffic Trends,'' ANI-0137121, $1,000,794 Sep 2002 - Aug 2005 (Claffy) As it grows, the Internet is becoming more fragile in many ways. The complexity in managing or repairing damage to the system can only be navigated with sustained understanding of the evolving commercial Internet infrastructure. The research and tools proposed under this effort lead to such insights. In particular, richer access to data will facilitate development of tools for navigation, analysis, and correlated visualization of massive network data sets and path specific performance and routing data that are critical to advancing both research and operational efforts. concentration of administration of Internet infrastructure.
``Routing and Peering Analysis for Enhancing Internet Performance and Security,'' ANI-0221172, $870,999 Oct 2002 - Sep 2005 (Claffy) CAIDA performs topology analysis and characterizes sources of growth and instability of the routing system, applying graph theory and comparing combinatorial approaches for identifying strategic locations in the macroscopic Internet.
References
- [1]
- T. Griffin, ``Position statement.'' Workshop on Internet Routing Evolution and Design (WIRED), October 2003. http://www.net.informatik.tu-muenchen.de/wired/position/griffin.html.
- [2]
- C. Wittbrodt, B. Woodcock, A. Ahuja, T. Li, V. Gill, and E. Chen, ``Global routing system scaling issues.'' NANOG Panel, February 2001. http://www.nanog.org/mtg-0102/witt.html.
- [3]
- G. Huston, ``Analyzing the Internet's BGP routing table,'' The Internet Protocol Journal, vol. 4, no. 1, 2001.
- [4]
- G. Huston, ``Scaling inter-domain routing-a view forward,'' The Internet Protocol Journal, vol. 4, no. 4, 2001.
- [5]
- G. Huston, Commentary on Inter-Domain Routing in the Internet. IETF, RFC 3221, 2001.
- [6]
- A. Doria, E. Davies, and F. Kastenholz, Requirements for Inter-Domain Routing. IRTF, Internet Draft, 2003.
- [7]
- A. Broido, E. Nemeth, and k claffy, ``Internet expansion, refinement, and churn,'' European Transactions on Telecommunications, vol. 13, no. 1, pp. 33-51, 2002.
- [8]
- D. Chang, R. Govindan, and J. Heidemann, ``An empirical study of router response to large BGP routing table load,'' in ACM SIGCOMM IMW, 2002.
- [9]
- D. Krioukov, K. Fall, and X. Yang, ``Compact routing on Internet-like graphs,'' in IEEE INFOCOM, 2004.
- [10]
- M. Thorup and U. Zwick, ``Compact routing schemes,'' in Proceedings of the 13th Annual ACM Symposium on Parallel Algorithms and Architectures (SPAA), pp. 1-10, ACM, 2001.
- [11]
- I. Castineyra, N. Chiappa, and M. Steenstrup, The Nimrod Routing Architecture. IETF, RFC 1992, 1996.
- [12]
- F. Kastenholz, ISLAY: A New Routing and Addressing Architecture. IRTF, Internet Draft, 2002.
- [13]
- NSF 04-540, ``Research in networking technology and systems (NeTS).'' Program Solicitation, April 2004. http://www.nsf.gov/pubs/2004/nsf04540/nsf04540.htm.
- [14]
- S. N. Dorogovtsev and J. F. F. Mendes, Evolution of Networks: From Biological Nets to the Internet and WWW. Oxford: Oxford University Press, 2003.
- [15]
- LightReading, ``Metro edge router test.'' http://www.lightreading.com/document.asp?doc_id=25454.
- [16]
- L. Kleinrock and F. Kamoun, ``Hierarchical routing for large networks: Performance evaluation and optimization,'' Computer Networks, vol. 1, pp. 155-174, 1977.
- [17]
- F. Heart, A. McKenzie, J. McQuillian, and D. Walden, ``ARPANET completion report,'' Technical Report 4799, BBN, January 1978.
- [18]
- D. Peleg, Distributed Computing: A Locality-Sensitive Approach. Philadelphia, PA: SIAM, 2000.
- [19]
- C. Gavoille, ``Routing in distributed networks: Overview and open problems,'' ACM SIGACT News - Distributed Computing Column, vol. 32, no. 1, pp. 36-52, 2001.
- [20]
- D. Krizanc, F. Luccio, and R. Raman, ``Compact routing schemes for dynamic ring networks,'' Technical Report 2002/26, Department of Mathematics and Computer Science, University of Leichester, 2002.
- [21]
- T. Griffin and G. Wilfong, ``An analysis of BGP convergence properties,'' in ACM SIGCOMM, 1999.
- [22]
- T. Griffin and G. Wilfong, ``Analysis of the MED oscillation problem in BGP,'' in IEEE ICNP, 2002.
- [23]
- Cisco, ``Endless BGP convergence problem in Cisco IOS software releases.'' Field Notice, October 2000. http://www.cisco.com/warp/public/770/fn12942.html.
- [24]
- D. McPherson, V. Gill, D. Walton, and A. Retana, BGP Persistent Route Oscillation Condition. IETF, Internet Draft, 2002.
- [25]
- D. Krioukov, K. Fall, and X. Yang, ``Compact routing on Internet-like graphs,'' Technical Report IRB-TR-03-010, Intel Research, 2003.
- [26]
- M. Faloutsos, P. Faloutsos, and C. Faloutsos, ``On power-law relationships of the Internet topology,'' in ACM SIGCOMM, pp. 251-262, 1999.
- [27]
- G. Siganos, M. Faloutsos, P. Faloutsos, and C. Faloutsos, ``Power-laws and the AS-level Internet topology,'' ACM/IEEE Transactions on Networking, vol. 11, no. 4, pp. 514-524, 2003.
- [28]
- A. Broido and k claffy, ``Internet topology: Connectivity of IP graphs,'' in SPIE International Symposium on Convergence of IT and Communication, 2001.
- [29]
- A. Lakhina, J. Byers, M. Crovella, and P. Xie, ``Sampling biases in IP topology measurements,'' in IEEE INFOCOM, 2003.
- [30]
- W. Willinger, R. Govindan, S. Jamin, V. Paxson, and S. Shenker, ``Scaling phenomena in the Internet: Critically examining criticality,'' PNAS, vol. 99, no. Suppl. 1, pp. 2573-2580, 2002.
- [31]
- Q. Chen, H. Chang, R. Govindan, S. Jamin, S. J. Shenker, and W. Willinger, ``The origin of power laws in Internet topologies revisited,'' in IEEE INFOCOM, 2002.
- [32]
- A. Vázquez, R. Pastor-Satorras, and A. Vespignani, ``Internet topology at the router and Autonomous System level,'' http://arxiv.org/abs/cond-mat/0112400.
- [33]
- P. Erdös and A. Réni, ``On random graphs,'' Publicationes Mathematicae, vol. 6, pp. 290-297, 1959.
- [34]
- S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhin, ``Metric structure of random networks,'' Nuclear Physics B, vol. 653, no. 3, pp. 307-422, 2003.
- [35]
- F. Chung and L. Lu, ``The average distance in a random graph with given expected degrees,'' Internet Mathematics, vol. 1, no. 1, pp. 91-114, 2003.
- [36]
- R. Cohen and S. Havlin, ``Scale-free networks are ultrasmall,'' Physical Review Letters, vol. 90, no. 05, p. 058701, 2003.
- [37]
- D. J. Watts and S. H. Strogatz, ``Collective dynamics of ``small-world'' networks,'' Nature, vol. 393, pp. 440-442, 1998.
- [38]
- H. Tangmunarunkit, R. Govindan, S. Jamin, S. Shenker, and W. Willinger, ``Network topology generators: Degree-based vs. structural,'' in ACM SIGCOMM, pp. 147-159, 2002.
- [39]
- T.Bu and D. Towsley, ``On distinguishing between Internet power law topology generators,'' in IEEE INFOCOM, 2002.
- [40]
- S. Zhou and R. J. Mondragon, ``Towards modelling the Internet topology - the Interactive Growth Model,'' in Proceedings of the 18th International Teletraffic Congress (ITC18), (Berlin), 2003. http://arxiv.org/abs/cs.NI/0303029.
- [41]
- H. Chang, S. Jamin, and W. Willinger, ``Internet connectivity at the AS level: An optimization driven modeling approach,'' in Proceedings of MoMeTools, 2003.
- [42]
- S. Zhou and R. J. Mondragon, ``Accurately modeling the Internet topology.'' http://arxiv.org/abs/cs.NI/0402011.
- [43]
- A.-L. Barabási and R. Albert, ``Emergence of scaling in random networks,'' Science, vol. 286, pp. 509-512, 1999.
- [44]
- R. Albert and A.-L. Barabási, ``Statistical mechanics of complex networks,'' Reviews of Modern Physics, vol. 74, pp. 47-97, 2002.
- [45]
- A. Vázquez, R. Pastor-Satorras, and A. Vespignani, ``Large-scale topological and dynamical properties of the Internet,'' Physical Review E, vol. 65, no. 06, p. 066130, 2002. http://arxiv.org/abs/cond-mat/0112400.
- [46]
- R. Albert and A.-L. Barabási, ``Topology of evolving networks: Local events and universality,'' Physical Review Letters, vol. 85, no. 24, p. 5234–5237, 2000.
- [47]
- G. Bianconi and A.-L. Barabási, ``Competition and multiscaling in evolving networks,'' Europhysics Letters, vol. 54, pp. 436-442, 2001.
- [48]
- A. Capocci, G. Caldarelli, R. Marchetti, and L. Pietronero, ``Growing dynamics of Internet providers,'' Physical Review E, vol. 64, p. 35105, 2001.
- [49]
- S. N. Dorogovtsev, A. V. Goltsev, and J. F. F. Mendes, ``Pseudofractal scale-free web,'' Physical Review E, vol. 65, no. 06, p. 066122, 2002.
- [50]
- S.-H. Yook, H. Jeong, and A.-L. Barabási, ``Modeling the Internet's large-scale topology,'' PNAS, vol. 99, pp. 13382-13386, 2002.
- [51]
- K.-I. Goh, B. Kahng, and D. Kim, ``Fluctuation-driven dynamics of the Internet topology,'' Physical Review Letters, vol. 88, p. 108701, 2002.
- [52]
- G. Caldarelli, A. Capocci, P. D. L. Rios, , and M. A. M. noz, ``Scale-free networks from varying vertex intrinsic fitness,'' Physical Review Letters, vol. 89, p. 258702, 2002.
- [53]
- G. Caldarelli, P. D. L. Rios, and L. Pietronero, ``Generalized Network Growth: from microscopic strategies to the real Internet properties.'' http://arxiv.org/abs/cond-mat/0307610.
- [54]
- H. Narayan, R. Govindan, and G. Varghese, ``The impact of address allocation and routing on the structure and implementation of routing tables,'' in ACM SIGCOMM, 2003.
- [55]
- ``Beyond BGP.'' Research Project. http://www.beyondbgp.net/.
- [56]
- CAIDA, ``Atomised routing.'' Research Project. https://www.caida.org/funding/atomized_routing/.
- [57]
- Internet Engineering Task Force (IETF), ``Site multihoming in IPv6.'' Working Group. http://www.ietf.org/html.charters/shim6-charter.html.
- [58]
- L. Cowen, ``Compact routing with minimum stretch,'' Journal of Algorithms, vol. 38, no. 1, pp. 170-183, 2001.
- [59]
- T. Eilam, C. Gavoille, and D. Peleg, ``Compact routing schemes with low stretch factor,'' Journal of Algorithms, vol. 46, pp. 97-114, 2003.
- [60]
- C. Gavoille and S. Pérennès, ``Memory requirement for routing in distributed networks,'' in Proceedings of the 15th Annual ACM Symposium on Principles of Distributed Computing (PODC), pp. 125-133, ACM, 1996.
- [61]
- C. Gavoille and M. Genegler, ``Space-efficiency for routing schemes of stretch factor three,'' Journal of Parallel and Distributed Computing, vol. 61, no. 5, pp. 679-687, 2001.
- [62]
- M. Thorup and U. Zwick, ``Approximate distance oracles,'' in Proceedings of the 33rd Annual ACM Symposium on Theory of Computing (STOC), pp. 183-192, ACM, 2001.
- [63]
- W. Aiello, F. Chung, and L. Lu, ``A random graph model for massive graphs,'' in Proceedings of the 32nd Annual ACM Symposium on Theory of Computing (STOC), pp. 171-180, ACM Press, 2000.
- [64]
- M. Arias, L. Cowen, K. A. Laing, R. Rajaraman, and O. Taka, ``Compact routing with name independence,'' in Proceedings of the 15th Annual ACM Symposium on Parallel Algorithms and Architectures (SPAA), pp. 184-192, ACM, 2003.
- [65]
- D. Krioukov, ``Project for a (r)evolution in data network routing: the Kleinrock universe and beyond,'' in MSRW, 2002.
- [66]
- Y. Afek, E. Gafni, and M. Ricklin, ``Upper and lower bounds for routing schemes in dynamic networks (abstract),'' in Proceedings of the 30th Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 370-375, IEEE, 1989.
- [67]
- B. Bollobás and O. Riordan, ``Mathematical results on scale-free random graphs,'' in Handbook of Graphs and Networks, (Berlin), Wiley-VCH, 2002.
- [68]
- k claffy, T. E. Monk, and D. McRobb, ``Internet tomography,'' Nature, January 1999. https://www.caida.org/catalog/software/skitter/.
- [69]
- B. Huffaker and M. Luckie, ``Scamper macroscopic Internet topology measurement tool,'' 2004. https://www.caida.org/catalog/software/scamper/.
- [70]
- kc claffy and B. Huffaker, ``Cisco URB 2003 proposal: Connectivity Ranking of Autonomous Systems,'' April 2003. https://www.caida.org/funding/cisco03asrank/.
- [71]
- kc claffy and B. Huffaker, ``Cisco URB 2004 proposal: Analysis & Visualization of IP Connectivity,'' April 2004. https://www.caida.org/funding/cisco04maps/.
- [72]
- The Cooperative Association for Internet Data Analysis (CAIDA). https://www.caida.org/.
- [73]
- CAIDA, ``Macroscopic topology measurements.'' Research Project. https://www.caida.org/projects/macroscopic/.
- [74]
- National Laboratory for Applied Network Research. http://www.nlanr.net/.
- [75]
- University of Oregon Route Views Project. http://www.routeviews.org/.
- [76]
- Y. Hyun, A. Broido, and k claffy, ``Traceroute and BGP AS path incongruities,'' in Cooperative Association for Internet Data Analysis (CAIDA), 2003. https://catalog.caida.org/paper/2003_asp.
- [77]
- Z. M. Mao, J. Rexford, J. Wang, and R. H. Katz, ``Towards an accurate ASlevel traceroute tool,'' in ACM SIGCOMM, 2003.
- [78]
- B. Huffaker, ``OWL: unified whois database,'' 2004. https://www.caida.org/tools/utilities/owl/.
- [79]
- CAIDA, ``rv2atoms.'' https://www.caida.org/funding/atomized_routing/download/.
- [80]
- G. Siganos and M. Faloutsos, ``Analyzing BGP policies: Methodology and tool,'' in IEEE INFOCOM, 2004.
- [81]
- M. E. J. Newman, ``A measure of betweenness centrality based on random walks.'' http://arxiv.org/abs/cond-mat/0309045.
- [82]
- H. Buhrman, J.-H. Hoepman, and P. Vitány, ``Space-efficient routing tables for almost all networks and the incompressibility method,'' SIAM Journal on Computing, vol. 28, no. 4, pp. 1414-1432, 1999.
- [83]
- H. Buhrman, M. Li, J. J. Tromp, and P. Vitányi, ``Kolmogorov random graphs and the incompressibility method,'' SIAM Journal on Computing, vol. 29, no. 2, pp. 590-599, 2000.
- [84]
- J. Körner, ``Coding of an information source having ambiguous alphabet and the entropy of graphs,'' in Transactions of the 6th Prague Conference on Information Theory, pp. 411-425, 1973.
- [85]
- J. Körner and A. Orlitsky, ``Zero-error information theory,'' IEEE Transactions on Information Theory, vol. 44, no. 6, pp. 2207-2229, 1998.
- [86]
- W. B. Norton, ``Internet Service Providers and peering.'' Equinix white paper. http://citeseer.ist.psu.edu/norton00internet.html.
- [87]
- L. Subramanian, S. Agarwal, J. Rexford, and R. H. Katz, ``Characterizing the Internet hierarchy from multiple vantage points,'' in IEEE INFOCOM, 2002.
- [88]
- A. Fabrikant, E. Koutsoupias, and C. H. Papadimitriou, ``Heuristically optimized trade-offs: A new paradigm for power laws in the Internet,'' in Proceeding of the 29th International Colloquium on Automata, Languages, and Programming (ICALP), vol. 2380 of Lecture Notes in Computer Science, pp. 110-122, Springer, 2002.
- [89]
- E. T. Jaynes, ``Information theory and statistical mechanics,'' Physical Review, vol. 106, pp. 620-230, 1957.
- [90]
- E. T. Jaynes, ``Information theory and statistical mechanics, II,'' Physical Review, vol. 108, pp. 171-190, 1957.
- [91]
- B. Leiner, V. Cerf, D. Clark, R. Kahn, L. Kleinrock, D. Lynch, J. Postel, L. Roberts, and S. Wolff, ``A brief history of the Internet,'' Communications of the ACM, vol. 40, no. 2, pp. 102-108, 1997.
- [92]
- Internet Engineering Task Force (IETF). http://www.ietf.org/.
- [93]
- The North American Network Operators' Group (NANOG). http://www.nanog.org/.
- [94]
- Internet Research Task Force (IRTF). http://www.irtf.org/.
- [95]
- IRTF Routing Research Group. https://irtf.org/groups.
- [96]
- Internet Research Task Force (IRTF), ``Routing research: Future domain routing scalability (RR-FS).'' Working Group. https://irtf.org.
- [97]
- CAIDA, ``Internet statistics and metrics analysis(ISMA).'' Workshop Series. https://www.caida.org/workshops/isma/.
- [98]
- N. Brownlee, ``Internet metrics Frequently Asked Questions (FAQ),'' Jan 2000. https://www.caida.org/outreach/metricswg/faq.xml.
- [99]
- CAIDA, ``Internet atlas project.'' https://www.caida.org/projects/internetatlas/.
Footnotes:
1The exact definition of the adaptation cost depends on the dynamic network model the scheme uses.
2Note that this definition follows the argument in [14] and is slightly different from the original definition in [37], which also requires strong clustering in a network.
3We chose PLRG because it was shown to produce the most realistic topologies among known Internet topology generators [38].
4We use the standard notation [O\tilde](x)=O(xlogO(1)(x)).
5Betweenness of a vertex is the relative number of shortest paths that pass through the vertex [81].
6The graph entropy defined in information theory (channel and source coding) by Körner [84] relates to a graph's chromatic number [85]: the fewest number of colors necessary to color the vertices of a graph so that no adjacent vertices are of the same color. This definition is not directly related to the Kolmogorov description complexity of the adjacency matrix, which measures a graph's ``randomness'' which is what interests us.
7Evocative models reproduce the observed phenomena. Explanatory models do the same, but they also ``close the loop''-they provide explanations for the observed phenomena, and further measurements can verify these explanations [30].
File translated from TEX by TTH, version 2.92.
On 15 Apr 2004, 14:26.
Additional Content
Toward Mathematically Rigorous Next-generation Routing Protocols for Realistic Network Topologies
CAIDA’s routing research focuses on applying key theoretical results in distributed computation theory to the development of protocols that will address issues of future Internet scalability.