---

1  Introduction

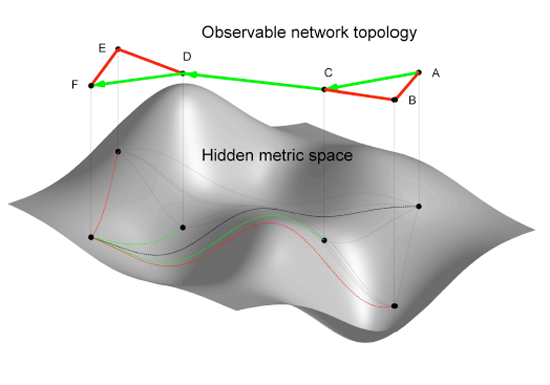
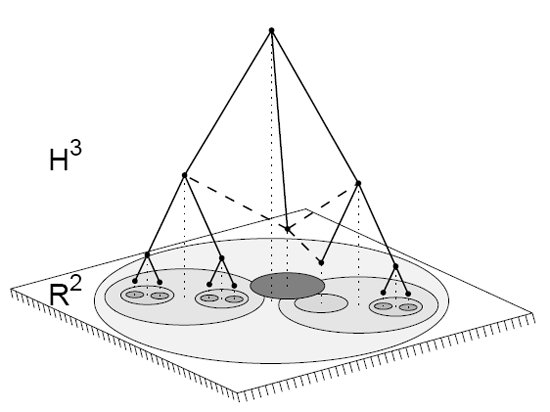
The lack of predictive power over complex systems, either designed by humans or evolved by nature, is a foundational problem in contemporary science [2]. The Internet offers a paradigmatic example: nothing inherent in the design of the Internet architecture [3] can explain the Internet's peculiar complex¹ large-scale structure [5], unexpectedly discovered decades after its inception. We are faced with an unsettling truth: the Internet topology has acquired emergent large-scale properties that are beyond our full understanding, much less control. The story is strikingly similar with the Web [6].

If the goal is to increase not only our understanding of complex networks, but also our ability to predict and engineer them, we believe the most promising direction is to study how this peculiar macroscopic structure relates to the function(s) of the network [4]. Our proposition is further strengthened by an astonishing fact: the peculiar structural characteristics of the Internet turn out to be eerily consistent with other complex networks found in nature, in particular with networks that exhibit naturally efficient, if not optimal, routing behavior without any global knowledge of network structure, e.g., neural and social networks [7,[8,[9].

This discovery poses a formidable intellectual challenge for network science and engineering. Conventional wisdom holds that finding communication paths to specific destinations through a network requires continually exchanging information about the status of connectivity between all nodes. The fundamentally unscalable overhead [10,[11] associated with this information exchange is built into our primary communication technologies today, including the Internet [12].

So we find it irresistibly interesting that so many other real networks in nature somehow "route traffic" efficiently without any global view of the system, i.e., nodes do not propagate any information about their connectivity status, but they efficiently find intended communication targets anyway. Our brains are a humbling example-to function they must successfully transmit specific signals to appropriate places in the body, but no neuron has a full view of global inter-neuron connectivity [7]. Milgram's experiments [8,[9] showed another classic demonstration of efficient routing without exchange of connectivity status information: humans can find paths to destinations through their social acquaintance network, even though no human has global knowledge of its structure. If man-made complex networks such as the Internet have a structure similar to so many networks in nature that can effectively route without global topology awareness, can network routing research take advantage of this efficiency?

In our previous project [13], primarily motivated by Internet routing scalability problems, we focused on this question, and introduced a new theoretical framework to support its study. Our framework generalizes Kleinberg's seminal explanation [14,[15,[16,[17] of Milgram's experiments. In that explanation, a network consists of two types of links: local and long-range. The long-range links exist with some probability, which depends on the shortest path distance between nodes in the subgraph composed of local links. This subgraph is called the local graph. In our approach, we generalize the local graph to be a hidden metric space. We call our spaces hidden because they play the role of an underlying coordinate system not readily observable by examining the network topology. Instead they use internal attributes of individual nodes to impose some navigable shape onto the network. By metric we mean that for each pair of nodes there is a non-negative distance between them defined, satisfying the triangle inequality. Specifically, the distance between two nodes in the hidden space reflects similarity in their intrinsic attributes, functional or structural [18,[19,[20,[21,[22,[23]. Nodes closer in the hidden space, i.e., more similar, are connected in the network topology with higher probability. This generalization of Kleinberg's approach allows for more flexible and realistic models of similarity spaces underlying real networks.

The described relationship between node similarity spaces and network topology also allows for a fundamentally different concept of routing. Without the overhead of maintaining topology knowledge, each node can forward information to its neighbor closest to the destination in the hidden space-a strategy known as greedy routing [14,[15,[16,[17], see Figure 1. Since this approach involves no traditional routing protocols or associated control plane, to be precise we will use the term greedy forwarding.

Figure 1: How hidden metric spaces influence the structure and function of complex networks. The smaller the distance between two nodes in the hidden metric space, the more similar they are, the more likely they are connected in the observable network topology. If node A is close to node B, and B is close to C, then A and C are necessarily close because of the triangle inequality in the metric space. Therefore, triangle ABC exists in the network topology with high probability, which explains the strong clustering observed in real complex networks. The hidden space also guides the greedy forwarding process: if node A wants to reach node F, it checks the hidden distances between F and its two neighbors B and C. Distance CF (shown by the curve lying on the surface) is smaller than BF, therefore A forwards information to C. Node C then performs similar calculations and selects its neighbor D as the next hop on the path to F. Node D is directly connected to F. The result is path A ® C ® D ® F shown by the arrowed edges in the observable topology. This path is the shortest path between A and F in the network.

The prospect of forwarding without routing is sufficiently attractive to motivate the following questions: do hidden metric spaces underlie the Internet, and if so, what are their key properties, how do we find them, and how efficient will greedy forwarding be when using them? Section 2 describes our recent discoveries: not only do metric spaces underlie real complex network topologies including the Internet [24], but a greedy routing mechanism applied to such topologies yields a maximum percentage of successful [1]- and almost always shortest [25]-paths, regardless of the structure of the hidden space. This explanation for why (if not how) complex networks are naturally navigable had sufficiently high interdisciplinary impact for recent publication in Nature [1].

However, even though all successful greedy paths are shortest, and their percentage is maximized for real network topologies, not all paths are successful. Some paths never reach destinations, getting stuck at local minima-nodes that do not have any neighbors closer to the destination than themselves. The percentage of successful paths depends not only on the network structure, but also on the structure of the hidden space, and on the relationship between the two structures. We know that hidden spaces are metric, but we have not yet studied their most basic geometric property-curvature. Spaces fall into three categories depending on their curvature K: Euclidean (K=0), spherical (K > 0), or hyperbolic (K < 0). We hypothesize that the geometry of complex networks is negative, i.e., that their hidden metric spaces are hyperbolic.

We propose exploring this hypothesis with three related tasks. First we will show analytically that the negative curvature of hidden hyperbolic geometries not only provides an explanation for the basic common structural properties of complex networks, but also optimizes an already efficient new approach to routing over such networks. Second, we will verify that hidden spaces underlying real networks are in fact negatively curved, and measure their basic geometric properties. Finally, our most challenging task will be to construct embeddings of the Internet and other complex networks into the identified hyperbolic spaces, such that greedy paths are shortest and successful even under dynamic network conditions. We outline our approach to these tasks in Section 3.

If successful, this project will fundamentally impact network science and engineering. Distributed topology knowledge and, consequently, routing updates would be unnecessary. Routing table sizes could be reduced to their theoretical minimum since instead of keeping a routing table entry for each destination in the network, nodes would be able to transmit information using only hidden space coordinates of their neighbors. We will have solved the two most fundamental routing scaling limitation of networks such as the Internet [12], and in the process created an essentially infinitely scalable routing architecture.

But our target of study is one of the most fundamental mysteries of all complex networks. The range of potential interdisciplinary applications (see Section 4) includes not only the Internet, but also recommender systems, search engines, terrorist network modeling, cancer and brain research, protein folding, and drug design.

Increasing predictive power over complex systems is our long-term objective. But we do not yet fully comprehend what laws govern the evolutionary dynamics of complex networks; we have only begun to identify their peculiar structure. If their structure is a result of natural evolution, we are interested in how this structure relates to their primary functions-are networks in nature optimizing toward information signaling (routing) efficiency? Discovery of the hidden metric spaces responsible for the primary function of many complex networks, i.e., communication without global knowledge, is the logical next step in our research agenda.

2  Previous work

Figure 2: Previous and proposed work, with logical dependencies.

Our proposed work builds on the success of our recently developed hidden metric space (HMS) framework [13]. Figure 2 depicts how our work is grounded by three results of that project:

Hidden metric spaces do exist. We found empirical evidence that hidden spaces do underlie real complex networks, and that these spaces are metric. We also showed that regardless of its specific structure, the HMS metric properties provide the only explanation thus far of clustering characteristics observed in real complex networks including the Internet [24]. The explanation is rather intuitive: the peculiar organization of triangles (transitivity of being connected) that comprise clustering in real networks is a reflection of the triangle inequality (transitivity of being close/similar) in the HMS.

Greedy paths are asymptotically shortest in complex network topologies. In [25] we proved analytically that regardless of the HMS structure, complex network topologies share a unique property: successful greedy paths are shortest in the limit of large network sizes. In other words, greedy forwarding is stretch-wise optimal (stretch is 1) on these topologies.

Topologies of real networks maximize the percentage of successful greedy paths. In [1] we used the simplest HMS model, a circle, to build an exhaustive set of synthetic networks. We found that more navigable networks, with higher ratios of successful greedy paths, have stronger clustering, and that their degree distributions have heavier tails. Many real complex networks including the Internet share these structural properties.

These results are encouraging, but leave some open questions. First, we must explore HMS models more sophisticated than a circle, chosen only for illustrative purposes rather than modeling capability. Circles, or more generally, spherical spaces, are unlikely to be the most appropriate models for HMSs under real networks. Appropriate models should explain both clustering and degree distribution shapes commonly observed in complex networks. Although in our previous work the clustering characteristics naturally emerged as a consequence of the fact that the circle is a metric space, we had to manually induce heavy-tailed degree distributions. More importantly, even though topologies of real networks, compared to other network topologies, corresponded to the maximum percentage of successful greedy paths over the circle HMS, this percentage was not 100%, but closer to 70%. Appropriate (and practically useful) HMS models should yield a percentage close to 100% on real networks. Finally, assuming we have an appropriate HMS model, we still must identify and measure the properties of real HMSs underlying real networks, how nodes in real networks compute and compare their HMS coordinates, and how network dynamics including link and node failures affect the efficiency of greedy forwarding. We will answer these and other questions in the work proposed below.

3  Proposed work

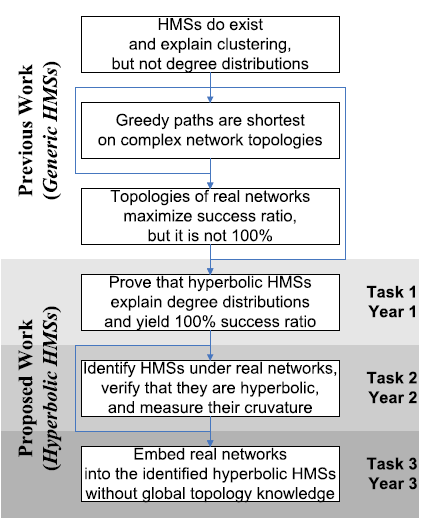
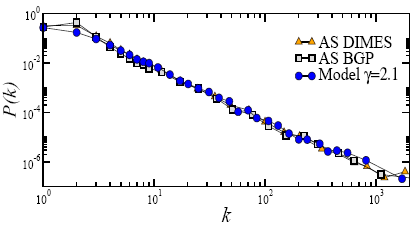
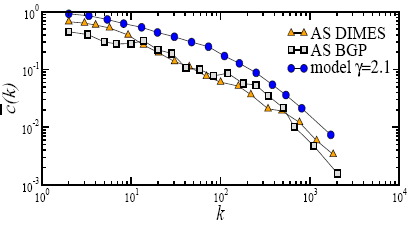
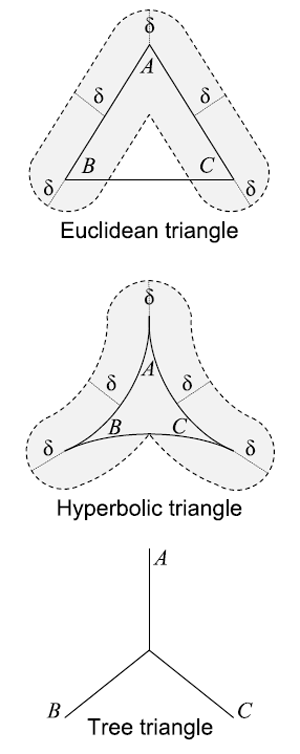
Our three tasks, shown in Figure 2, involve analytic proofs, measurement and data analysis, and model construction and validation. Task 1 is to gain mathematical knowledge of how specific geometric properties of hyperbolic spaces are manifested in observed networks. Completion of Task 1 will allow us to explore node similarity spaces underlying real networks, verify that they are hyperbolic, and measure their geometric properties, such as curvature (Task 2). Knowledge of what spaces to look for (obtained from Task 2) will lead to our ultimate goal-embedding of real networks into the identified hyperbolic spaces, such that greedy paths are shortest and successful even under dynamic network conditions. Before we describe these tasks in detail, we motivate our central hypothesis that hidden spaces are hyperbolic.

Motivation for hyperbolic HMSs. The intuitive explanation for the power of hyperbolic geometry to abstract node similarity spaces lies in the observation that complex networks are systems of connections between heterogeneous nodes. Heterogeneity implies that in reality nodes can be classified into groups, subgroups, subsubgroups, and so on. This taxonomy of nodes naturally results in a tree-like structure akin to a library catalog, in which the distance between two nodes estimates how similar they are [18,[23]. Such tree-like structures are known to be hyperbolic, i.e., negatively curved [26]. The node classification hierarchy need not be strictly a tree. Approximate "tree-ness" is sufficient for hyperbolic representation [26].

Mathematically, the last statement is rooted in the main property of hyperbolic geometry-exponential expansion of space [27]. Figure 3 illustrates the Poincaré disc model [28] of the hyperbolic plane, which is the two-dimensional space of constant curvature K=-1. The area of a disc of hyperbolic radius R grows as e^R in the hyperbolic plane [28]. But trees possess essentially the same metric structure as the hyperbolic plane. In a b-ary tree, i.e., a tree with branching factor b, the volume of a ball of radius R, measured as the number of nodes lying within R hops from the root, grows as b^R. From the purely metric perspective, the hyperbolic plane is thus equivalent to a tree with the average branching factor equal to e. Informally, hyperbolic spaces can be thought of as "continuous versions" of trees. This metric equivalence between hyperbolic spaces and tree-like structures, which naturally abstract taxonomy-based similarities among heterogeneous nodes, explains why hyperbolic geometry is a promising model for HMSs underlying complex networks.

3.1  Task 1: Prove analytically that hyperbolic geometries are the most congruent with complex network topologies

Figure 3: Artistic visualization of the hyperbolic plane by Silvio Levy, based on M. C. Escher's Circle Limit III, with the permission from the Geometry Center, University of Minnesota. The exponential expansion of fish illustrates the exponential expansion of hyperbolic space. All fish are of the same hyperbolic size, but their Euclidean size exponentially decreases, while their number exponentially increases with the distance from the origin.

We say that a network topology is more congruent with its HMS, the higher the efficiency of greedy forwarding, and the richer the set of HMS-explained topological properties. The goal of this task is to provide mathematical proofs that hyperbolic HMSs naturally explain all basic common properties of complex network topologies, and that the efficiency of greedy forwarding in these topologies with underlying hyperbolic HMSs achieves its theoretical maximum. For the analytic part, we will use tools from hyperbolic geometry, statistics, statistical mechanics, and graph theory. To confirm our analytic results with simulations, we will use computer clusters at UC, San Diego, and the University of Barcelona.

Our methodology consists of the following steps: (1) graph construction: distribute nodes in a given hyperbolic space according to some node density function; connect distributed nodes according to some connection probability function, which specifies the probability that two nodes located at a given hidden distance are connected; (2) calculate the topological properties of the resulting graphs, and compare them with real network topologies; and (3) calculate the efficiency metrics of various greedy forwarding algorithms in the resulting graphs. Below we describe the components of this methodology.

Hyperbolic space models. We will study models of hyperbolic spaces of different dimensions and curvatures. There are several important isometric models of hyperbolic space of constant curvature K=-1: the Poincaré ball and half-space model, the Klein model, the Lorentz hyperboloid model, etc. [29]. The curvature can also be some other negative constant, or vary throughout the space [30].

Node density. The simplest node density is uniform within a hyperbolic ball. Since the hyperbolic space expands exponentially, the hyperbolically uniform density is exponential from the Euclidean perspective. Natural candidates for other, non-uniform densities are also exponential, but with different values of the exponent. The hyperbolic ball can have a fixed radius, or the radius can increase with the number of nodes.

Connection probability. There are several candidates for the connection probability function, which can be a step function or decrease exponentially with the hidden distance between nodes. These two candidates are most natural among many possibilities.

Graph metrics. To analyze the topology of a modeled graph and to compare it with observed topologies, we will use the basic dK-properties from our previous work [31]: degree distribution, correlation, clustering, etc.

Greedy forwarding algorithms. We will measure the efficiency of various greedy forwarding algorithms on static networks and under dynamic scenarios with node and link failures. In the simplest possible greedy forwarding algorithm a packet is forwarded from the origin node to the destination node via a series of intermediate nodes (see Figure 1). The current hop node selects as the next hop node the neighbor closest to the destination in the hyperbolic space, and drops the packet if the current hop node is a local minimum, meaning that it has no neighbor closer to the destination than itself. An example modification to this algorithm is geodesic forwarding, where the current hop selects, among all its downstream neighbors, the one closest to the hyperbolic geodesic connecting itself (or the source) and the destination. As in the Euclidean space, the hyperbolic geodesic is the shortest hyperbolic line connecting two points [28].

Efficiency metrics of greedy forwarding. The first metric is the success ratio: the percentage of greedy paths that successfully reach their destinations before getting stuck at any local minima. Another class of metrics is related to stretch, which measures how much longer than the shortest paths the greedy paths are. We will study two types of stretch: one related to the shortest paths in the graph, the other-to the hyperbolic geodesics.

Figure 4: Degree distribution P(k) ~ k -g and degree-dependent clustering [`c](k) in synthetic graphs, juxtaposed against the same metrics for the AS topologies from RouteViews [32] and DIMES [33].

Preliminary experiments. We have performed preliminary numeric experiments, using the Poincaré disc of constant curvature K=-1, the simplest node distribution (uniform within a ball of hyperbolic radius proportional to the logarithm of a given number of nodes), and the simplest connection probability function (step function). Figure 4 shows that this construction yields synthetic graphs (labeled Model in the legend) with strong clustering and a heavy-tailed degree distribution, virtually identical in these properties to two data sets of the Internet AS topology. In contrast to our earlier work [1], here heavy tails emerge naturally; we do nothing to enforce them. That is, the fact that the hidden space is metric explains strong clustering, and the fact that it is hyperbolic appears to give rise to a heavy-tailed degree distribution. We have also found numerically that 99% of greedy paths in these synthetic graphs are successful, and all successful paths are shortest.

To summarize, for Task 1 we will pursue three results: (1) establish and prove explicit mathematical relationships between the properties of hyperbolic HMSs, e.g., curvature, dimension, node density, connection probability, etc., and the properties of the resulting graphs, e.g., their degree distribution, clustering, etc.; (2) calculate analytically the efficiency metrics of different greedy forwarding algorithms in these synthetic graphs; and (3) study how these efficiency metrics deteriorate under network dynamics, i.e., when links or nodes die and reappear.

3.2  Task 2: Measure geometric properties of hyperbolic spaces hidden under real networks

In Task 1 we start with a continuous hyperbolic space, and then distribute nodes in it to build a synthetic network. The hidden distances between these nodes form a finite metric space. In Task 2, we explore the reverse problem: starting with the finite metric space formed by the similarity distances between nodes in a real network, we infer the properties of a corresponding underlying continuous space, verify that it is hyperbolic, and then relate its geometric properties to the network's topological properties, using the mathematical apparatus developed in Task 1.

Figure 5: The d-neighborhood of the union of triangle sides AB and AC contains side BC in hyperbolic geometry, but not in Euclidean one. In trees, the union of AB and AC fully contains BC.

Similarity metrics. There is no shortage of similarity metrics in the literature, e.g., cosine similarity, Jaccard coefficient, Jensen-Shannon divergence, etc. [34]. They all reduce the comparison of nodes to comparison of some attributes of the nodes. These attributes can be a collection of sets or communities. For example, each node i, i=1,¼,n, can belong or not belong to communities j, j=1,¼,m. To compute the cosine similarity between nodes, we map each node i to vector v_i Î R^m whose jth component is 1 if i belongs to community j, or 0 otherwise. The cosine similarity distance between i and i¢ is then d _ii¢ =1-cosq _ii¢ , where q _ii¢ is the angle between v_i and v _i¢ , cosq _ii¢ =[(v_i  ·  v _i¢ )/(||v_i||·||v _i¢ ||)]. To see if our results are consistent, we will test as many applicable similarity metrics as possible, for each network.

Networks to consider. We can consider any network with some node attribute data, i.e., networks in which nodes are classified by annotations of network-specific attributes. In particular, we will consider the following networks. (i) AS Internet. In our previous work [35] we classified ASes based on their business roles, content of their WHOIS records, estimated number and type of customers, providers, peers, and advertised IP prefixes, geographic location and coverage, etc. (ii) Social networks. Many social networks have explicit node community data available, which makes them easier to study than the Internet topology, where business relationships are confidential, and their inference is prone to errors [36,[37,[38]. In the Wikipedia social network [22], for example, nodes are editors, and communities are articles. Editor i belongs to community j if he edited article j. The jth component of vector v_i is equal not to either 0 or 1, but to the number of times i edited j. Computing the cosine similarity between editors thus allows us to capture editing activity as well as similarity of editors. (iii) Web. Nodes are web pages, communities are words. If page i has x occurrences of word j, then the jth component of v_i is x [20]. (iv) Biological networks. Many biological networks have rich annotations amenable to similarity computations. For example, in cell regulatory networks there are established techniques to compute similarities between genes or proteins [39]. (v) Other networks. In networks where it is not immediately clear how to compute node similarities, we will use generic community structure detection algorithms [19,[23,[40,[41]. A good example of such a network is the network of PGP trust relationships [42]. The available data does not reveal any explicit communities; it contains only connectivity information representing mutual trust.

Identifying the hidden space. Having computed the finite space of node similarities, we will determine whether this space is metric, whether its underlying continuous space is hyperbolic, and if so, estimate its curvature. Testing whether the finite space is metric requires only checking how often the triangle inequality is violated. The underlying space is hyperbolic if the distribution of distances grows exponentially. It is impossible to have an exponentially growing distance distribution between a finite number of nodes located in a Euclidean or spherical space, even with exponential node densities, but the uniform node density in any hyperbolic space produces such exponential distance distributions [43]. Estimating curvature is the most complicated-there is no direct way to infer curvature of an underlying continuous space from the metric space formed by the distances among a finite number of nodes in it. To handle this challenge we propose the following new methodology based on Gromov's d-hyperbolic spaces.

Gromov's d-hyperbolic spaces. Gromov [44] defines a metric space to be d-hyperbolic if for each four nodes w,x,y,z the distances between them satisfy d(w,z)+d(x,y) £ d(w,y)+d(x,z)+d, assuming that they are ordered such that d(w,x)+d(y,z) £ d(w,y)+d(x,z) £ d(w,z)+d(x,y). This d-hyperbolic condition reflects another fundamental property of hyperbolic spaces: triangles are thin in them. Each side of any, even arbitrarily large, hyperbolic triangle is contained within a d-neighborhood of the union of other two sides [28], illustrated in Figure 5. The exponential expansion of space follows from this d-hyperbolic condition [44,[26].

Figure 6: The exponential PDF of similarity distances in the Wikipedia editor social network [45,[22] suggests a hyperbolic space underlying the network.

Generally, the smaller the d, the "more hyperbolic" the space. Trees are 0-hyperbolic. Informally, their "curvature" is -¥. The triangles in trees are subtrees, therefore each side is fully contained within the union of two other sides. Euclidean spaces, whose curvature is 0, are ¥-hyperbolic-infinitely large triangles have points on their different sides that are infinitely far apart. Knowing d will allow us to estimate the curvature of the underlying space because the d of a hyperbolic space of curvature K < 0 is given by d = ln(1+Ö2)/Ö{-K} [39,[28,[30]. The d-hyperbolic property also applies to finite metric spaces [46,[47,[48]. In fact, any finite metric space is d-hyperbolic with d equal to the diameter of the finite space. Its underlying continuous space is hyperbolic if d is characteristically smaller than the finite space diameter [47,[48].

We will estimate d of the underlying HMS using the following procedure. We will first calculate the similarity distances between all pairs of nodes, e.g., d _ii¢ =1-cosq _ii¢ . We will then consider random balls of increasing sizes n. For each n, we will randomly select a set of nodes, ball centers, and for each center, find the n nodes closest to it, i.e., its n-sized ball. Considering all 4-node combinations in each ball, we will measure its d using Gromov's d-hyperbolic condition. We will then find the average d(n) across all n-sized balls. Then we will increase n, and repeat the same procedure. If d(n) saturates at some specific value before n reaches the network size, this d-value reflects the d of the underlying space, and consequently its curvature, which we will relate to the observable network structure using the results of Task 1.

Preliminary experiments. Thanks to David Crandall and Jon Kleinberg who shared their data from [22] with us, Figure 6 shows the similarity distance distribution in the social network of Wikipedia editors. The network nodes are editors, and two nodes are assumed to be connected in [22] if one editor posted to the other's discussion page. The node degree distribution follows a bi-modal power law (not shown). The hidden social distance between two editors i and i¢ is their cosine similarity distance d _ii¢ discussed above. Figure 6 shows an exponential distribution of these social distances between editors, even hyper-exponential for large distances, i.e., the similarity space is hyperbolic.

3.3  Task 3: Construct embeddings of real networks into the identified hyperbolic spaces requiring no global knowledge of network topologies

Figure 7: Mapping between discs in the Euclidean plane R2 and points in the hyperbolic space H3. The x,y-coordinates of discs in R2 are the x,y-coordinates of the corresponding points in H3. The z-coordinates of these points in H3 are the radii of the corresponding discs. This mapping represents the tree-like hierarchy among the discs. Two points in H3 are connected by a solid link if one of the corresponding discs is the minimum-size disc that fully contains the other disc. This hierarchy is not perfect, thus the tree structure is approximate. The darkest disc in the middle partially overlaps with three other discs at different levels of the hierarchy. Two points in H3 are connected by a dashed link if the corresponding discs partially overlap. These links add cycles to the tree. The shown structure is thus not strictly a tree, but it is hyperbolic [26].

Completion of Task 2 will reveal the basic properties of the hyperbolic HMS underlying real networks. In Task 3 we address the problem of how nodes in a real network can compute their coordinates in the identified HMS without any global topology knowledge. If nodes know the topology of their network, then the technique from [49] would allow them to easily find their coordinates in the hyperbolic plane such that greedy forwarding is 100%-successful, but this technique does not guarantee that resulting greedy paths are shortest; in fact, their stretch is unbounded in [49]. More importantly, this technique requires global topology knowledge, leading to the communication overhead we are trying to avoid.

Similarities between community sets vs. hyperbolic distances between nodes. In Task 2 we explore how hyperbolic distances serve as a natural measure of similarity between sets of communities in real networks. Recall that in order to compute the cosine similarity between nodes, we first map each node to a vector representing the set of communities to which the node belongs, i.e., the set of attributes that characterize the node, and then compare the vectors by the cosine of the angle between them. The more two sets overlap, i.e., the stronger the similarity, the smaller the angle between the corresponding vectors.

Why does hyperbolic geometry naturally emerge from similarity measures such as cosine similarity? Figure 7 illustrates the connection. The Euclidean discs in R² represent abstract sets of communities. Each disc in R² is mapped as shown to a node in the Poincaré half-space model of the 3-dimensional hyperbolic space H³ [28]. Colloquially, we call two discs similar if their radii are similar and centers are close to each other in R². The shown mapping turns out to be such that if two discs in R² are similar, then the two nodes representing them in H³ are hyperbolically close, and vice-versa. Formally, if the ratio of the discs' radii r,r¢ is bounded by a constant C, 1/C £ r/r¢ £ C, and the Euclidean distance between their centers is bounded by Cr, then one can show [26] that the hyperbolic distance between their corresponding nodes in H³ is bounded by some constant C¢, which depends only on C, and not on the disc radii or center locations. The converse is also true. Therefore, similarity distances between community sets and hyperbolic distances between the corresponding nodes are congruent measures.

Having the hyperbolic HMS identified for a concrete real network, we will map, or embed, nodes into this HMS using the general prescription above, if needed with additional network annotation specifics. We will apply this prescription with minor modifications to the AS Internet.

AS embedding. One of the most important AS attributes is the geographic coverage of operations of an AS [50,[51]. We will use this attribute for AS embedding by first computing the minimum-size geographic disc covering the geographic scope of the AS's presence of operations, and then map this disc to the hyperbolic HMS in a way similar to that described in Figure 7. The only difference is that the Earth's surface is not Euclidean but spherical, and therefore we must use the ball model of H³ [28]. We emphasize that this construction does not require any global knowledge. All information necessary for an AS to compute its hyperbolic coordinates is available to the AS; no information exchange with other ASes is needed. However, this information is not readily available to us, so we will estimate the geographical scope by sufficiently sampling the IP address space advertised by each AS, and mapping each sampled IP address to its geolocation using commercially available IP geolocation technology [52]. The resulting approximation of the geographic extent of each AS's operations will determine the minimum-size geographic discs, or other geometric sets [53], to use for the embedding in Figure 7.

The proposed embedding naturally takes care of the AS sizes and the AS hierarchy that they induce. Larger ASes have wider geographic coverage, and hence map to larger discs, which in turn map to higher nodes in Figure 7, i.e., nodes with larger z-coordinates, located closer to the top of the shown hierarchy. We see that geography contributes to the HMS structure in a peculiar way, inducing the hidden negative curvature. It is instructive to compare this construction to geographic routing [54,[55,[56,[57,[58], where geography is a non-hidden Euclidean metric space.

Greedy forwarding compliant with routing policies. Once we embed the AS graph into its hyperbolic HMS, we will measure the efficiency metrics of greedy forwarding in this embedding. In addition, we will measure the percentage of greedy paths that comply with routing policies, i.e., with AS relationships inferred in our previous work [38]. We expect this percentage to be high because many policy compliant paths [36,[37,[38] and greedy paths [1] are congruent. They follow the same hierarchical path pattern, propagating from low-degree sources to high-degree hubs in the core (customer-to-provider segments), and then to low-degree destinations (provider-to-customer segments). We will handle non-compliant paths (if any) using the policy bit technique from [59], i.e., in the beginning of the path, greedy forwarding is allowed to follow any link, but once a peer-to-peer or provider-to-customer link is crossed, the policy bit in the packet header records this event, and for the remainder of the path only provider-to-customer links are allowed.

AS topology dynamics and growth. Our ultimate goal is to eliminate or minimize routing overhead, even under dynamic network conditions. If a link fails, greedy forwarding must find an alternative path without any information exchange about the failure. The two factors that make such forwarding without routing updates possible are high path diversity in the AS topology [60] and congruency between the shortest and greedy paths mentioned above. Since there are many disjoint shortest paths between the same source and destination, even if a link belonging to one path fails, many other paths remain, and greedy forwarding can still find them since all of them are close to the same hyperbolic geodesic. This phenomenon is difficult to visualize in Euclidean space, but intuitively, hyperbolic spaces have exponentially "more space," so exponentially more paths can be near the same geodesic, compared to the Euclidean case.

To replicate realistic AS topology dynamics at short time scales (link/node failures) we will use the finest-grain BGP data available, and then measure how the dynamics affect the efficiency metrics of greedy forwarding. If the success ratio is not exactly 1, we will adjust the embedding using additional AS attributes, maximum likelihood methods akin to those in [23], and other greedy forwarding modification techniques [61,[62,[63,[64,[65,[66,[67,[68,[69].

We will also study how AS topology evolution over long time scales (years), i.e., its historical growth [70], affects the quality of our embedding and greedy forwarding. Specifically, we will embed an AS topology from ten years ago and replay its growth using historical time series data [70]. We will add new ASes as our embedding prescribes, but keep existing AS HMS coordinates the same. If the AS topology changes significantly, we expect greedy forwarding efficiency will deteriorate noticeably. We will measure how quickly greedy forwarding error accumulates over time, so we can ascertain how frequently all existing ASes should recompute their HMSs coordinates in order to maintain greedy forwarding efficiency.

Figure 8: The scatter plot of the hyperbolic distance to the destination vs. the logarithm of node degree for all hops of the successful paths in the simplest AS embedding. The shown paths are between sources and destinations lying at large hyperbolic distances comparable with the hyperbolic ball diameter.

Preliminary experiments. Inspired by our design of the AScore poster [71], we have experimented with an AS embedding that is much easier to implement than the one described above. We map each AS to a point in H³, such that the angular components of each point are equal to the latitude and longitude of the headquarters of the corresponding AS extracted from its WHOIS record, and the radial component is equal to the radial component of nodes of the corresponding degree in our simplest possible model in Task 1. This embedding is the simplest but also the crudest possible, ignoring all network details. Nevertheless, our first experiments with greedy forwarding using this embedding yielded a non-trivial success ratio of 26%. For comparison, embedding of random graphs yields the success ratio of 0.3%. Even more encouraging is Figure 8, which shows the pattern of the hyperbolically longest successful greedy paths in this embedding. Most hops are at low-degree nodes close to the sources and (less so) destinations, and at high-degree nodes in the middle of paths. The paths thus exhibit the navigable hierarchical path pattern mentioned above and discussed in detail in [1]. This pattern indicates that the AS Internet is naturally navigable, and what remains is to find the right embedding so greedy forwarding can take advantage of this navigability.

4  Interdisciplinary aspects and potential applications

Although our original motivation for embedding complex networks in geometric spaces was to design scalable routing for the Internet, this project will expand the utility of our theoretical framework to a broad range of interdisciplinary applications in network science and engineering beyond the proposed scope of work.

Searching and navigation strategies. The most direct application of navigation is search. Searching for specific nodes is a task that arises in many networks. One can search for specific individuals, e.g., terrorists [72,[73,[74], in traditional or on-line social networks (cf. Milgram's experiments [8,[9]), for specific content on the Web or overlay/P2P networks, for specific knowledge in Wikipedia or paper citation networks. Discovery of the HMSs underlying these systems can improve the quality of existing search engines, and lead to designing future ones.

Recommender systems. Recommender systems [75,[76] are closely related to search. To recommend a product that a user might like, they estimate similarities among users, e.g., among book buyers at Amazon or DVD renters at Netflix. These systems assume that similar users tend to like similar products or content. Often these similarity spaces are embedded in Euclidean spaces to enable navigation [77]. Finding more congruent hyperbolic embeddings for these similarity spaces could significantly improve the quality of such recommender systems and the efficiency of navigation (browsing).

Discovery of missing and false links. Topology measurements of many real networks, not only of the Internet [78,[79,[80,[81], miss some links, and contain some false ones [82,[83,[84,[85,[86]. Missing links can be a critical problem, for example in networks of terrorist or protein interactions [84,[85,[86]. Knowledge of the HMS and connection probability for a network helps to predict missing and false links [23].

Systems biology: cancer and brain research. A great deal of cancer research studies signaling pathways in the gene regulatory networks [87,[88,[89]. The main process in the brain is also signal propagation [7,[90,[91]. Propagation of cellular and neural information are two paradigmatic examples of navigation without global knowledge. Understanding how HMSs effectively guide these navigation processes, including which functional network components correspond to specific neighborhoods in the HMS, can significantly advance studies of cancer and the brain.

Cognitive science: memory and consciousness. Natural language is a translation of semantic concepts in the brain into external lexical representations. Cognitive science studies what sources of statistical information are relevant in psycholinguistic processes. This research has introduced semantic space models to formalize the cognitive processes we use to organize, store and retrieve information [92,[93,[94,[95,[96]. The semantic similarity between two words is the cosine similarity of the vectors representing these words in the semantic space. Finding accurate representations of these underlying spaces can contribute to research on cognitive processes as emergent complex phenomena.

Protein folding and drug design. At a workshop [97] organized for our previous project [13], we learned an unexpected application of greedy forwarding over an HMS-protein folding [98,[99], a critical component in the design of new drugs [100]. In this case, the HMS is a protein conformation free energy profile, nodes are protein conformations, and two conformations are connected if they can be obtained from each other by one amino-acid rotation. Protein folding is then equivalent to greedy forwarding toward the minimum-energy conformation [99]. The discovery of a protein folding HMS is thus equivalent to the description of its energy profile.

Wireless and social networking. Our HMS framework applied as is to traditional wireless networking becomes well-known geographic routing [54,[55,[56,[57,[58]. But the underlying geographic space is neither hidden nor hyperbolic, distances in it do not reflect any node similarities, and wireless network topologies do not resemble complex network topologies [101]. Most importantly, there is no congruency between node flat ID addressing and the underlying geography, unless nodes dynamically learn and redistribute the information about their positions, which for large networks involves exactly the enormous communication overhead that prevents scaling. Therefore the applicability of HMSs, especially hyperbolic ones, to traditional wireless networking is not obvious.

Nevertheless, we believe our framework can be useful for emerging models of wireless networks, in which the "social overlay" guides forwarding [102,[103,[104,[105,[106]. In these models, the destination of information propagation is a specific individual or content. Forwarding decisions rely on social distances to the destination, while network connectivity is provided by the highly dynamic "wireless underlay." The HMSs in this case are social distance spaces, which we hypothesize (and explore in Task 2) are hyperbolic.

5  Broader impacts

Complex networks are ubiquitous in all domains of science and engineering, and permeate many aspects of daily human life, from biological to social, economic, transportation, and communication [107]. Our growing dependence on networks has inspired a burst of activity in the new field of network science [2], keeping researchers motivated to solve the difficult challenges that networks offer. Among these, the relation between network structure and function is perhaps the most important and fundamental [4].

Transport is one of the most common functions of networked systems. Examples span many domains: transport of energy in metabolic networks, of mass in food webs, of wealth, funds, and products in economic networks, of people in transportation systems, or of information in cell signaling processes and, of course, across the Internet. Although our motivating focus is information transport in the Internet, we are aiming directly at the most fundamental mysteries of complex networks. Therefore our results may have broad and lasting impact on many sciences and disciplines. Our work will also cross-fertilize networking, theoretical computer science, physics, and mathematics, as our approach relies on tools and techniques from all these disciplines. Our agenda is thus directly responsive to the need for interdisciplinary advances articulated by NSF in this program solicitation.

In addition to publishing our results via conferences, journals, and on the web, we will present to network engineering groups (IETF, IRTF), as well as in academic research venues and visits. PI Krioukov presented results at several universities worldwide in 2008 [108], finding several students interested in the proposed work. We will host an interdisciplinary workshop during this project, building on the success of related previous workshops [109,[97], with new focus on the boundaries and relationships among science, engineering, economics, and policy constraints.

PI Krioukov is an editorial board member of the ACM SIGCOMM Computer Communication Review. He has served as a PC member at SIGCOMMs, CoNext, NetSciCom, SIMPLEX, and other venues, and regularly reviews for IEEE/ACM Transactions on Networking. PI Claffy is on the program committee for PAM 2009, Internet2's Research Advisory Council, and ICANN's Security and Stability Committee. UC Boguñá reviews for Physical Review Letters, Physical Review E, Journal of Statistical Physics, among others. In 2008 he received the Outstanding Referee Award [110] from the American Physical Society. UC Serrano is also a regular referee for many of the top physics journals. In 2009 she won a prestigious Ramón y Cajal award from the Spanish Ministry of Science, and is developing a research agenda in Systems Biology, which will strengthen the interdisciplinary aspects and potential applications of this project.

The project improves the presence of under-represented groups in science. Two senior members on this proposal (PI Claffy and UC Serrano) are females. PI Krioukov co-advised female PhD students Priya Mahadevan and Almerima Jamakovic who successfully moved to HP Labs and TNO after their graduation. PIs Claffy and Krioukov regularly work with an NSF-sponsored Research Experiences for Undergraduates (REU) program to mentor under-represented undergraduates from UCSD and other universities, giving students invaluable early experience in Internet research.

References

[1]

M. Boguñá, D. Krioukov, and kc claffy, "Navigability of complex networks," Nature Physics, vol. 5, pp. 74-80, 2009.

[2]

C. B. Duke, ed., Network Science. Washington: The National Academies Press, 2006.

[3]

D. Clark, "The design philosophy of the DARPA Internet protocols," in SIGCOMM, 1988.

[4]

M. E. J. Newman, "The structure and function of complex networks," SIAM Rev, vol. 45, no. 2, pp. 167-256, 2003.

[5]

M. Faloutsos, P. Faloutsos, and C. Faloutsos, "On power-law relationships of the Internet topology," in SIGCOMM, 1999.

[6]

J. Hendler, N. Shadbolt, W. Hall, T. Berners-Lee, and D. Weitzner, "Web science: An interdisciplinary approach to understanding the Web," Commun ACM, vol. 51, no. 7, pp. 60-69, 2008.

[7]

P. Churchland and T. J. Sejnowski, The Computational Brain. Boston: The MIT Press, 1994.

[8]

S. Milgram, "The small world problem," Psychol Today, vol. 1, pp. 61-67, 1967.

[9]

J. Travers and S. Milgram, "An experimental study of the small world problem," Sociometry, vol. 32, pp. 425-443, 1969.

[10]

A. Korman and D. Peleg, "Dynamic routing schemes for general graphs," in ICALP, 2006.

[11]

D. Krioukov, kc claffy, K. Fall, and A. Brady, "On compact routing for the Internet," Comput Commun Rev, vol. 37, no. 3, pp. 41-52, 2007.

[12]

D. Meyer, L. Zhang, and K. Fall, "Report from the IAB workshop on routing and addressing." IETF, RFC 4984, 2007.

[13]

CAIDA, "NeTS-FIND: Greedy routing on hidden metric spaces as a foundation of scalable routing architectures without topology updates." Research Project. https://www.caida.org/funding/nets-find/.

[14]

J. Kleinberg, "Navigation in a small world," Nature, vol. 406, p. 845, 2000.

[15]

J. Kleinberg, "The small-world phenomenon: An algorithmic perspective," in STOC, 2000.

[16]

J. Kleinberg, "Small-world phenomena and the dynamics of information," in NIPS, 2001.

[17]

J. Kleinberg, "Complex networks and decentralized search algorithms," in ICM, 2006.

[18]

D. J. Watts, P. S. Dodds, and M. E. J. Newman, "Identity and search in social networks," Science, vol. 296, pp. 1302-1305, 2002.

[19]

M. Girvan and M. E. J. Newman, "Community structure in social and biological networks," Proc Natl Acad Sci USA, vol. 99, pp. 7821-7826, 2002.

[20]

F. Menczer, "Growing and navigating the small world Web by local content," Proc Natl Acad Sci USA, vol. 99, pp. 14014-14019, 2002.

[21]

E. A. Leicht, P. Holme, and M. E. J. Newman, "Vertex similarity in networks," Phys Rev E, vol. 73, p. 026120, 2006.

[22]

D. Crandall, D. Cosley, D. Huttenlocher, J. Kleinberg, and S. Suri, "Feedback effects between similarity and social influence in online communities," in KDD, 2008.

[23]

A. Clauset, C. Moore, and M. E. J. Newman, "Hierarchical structure and the prediction of missing links in networks," Nature, vol. 453, pp. 98-101, 2008.

[24]

M. Á. Serrano, D. Krioukov, and M. Boguñá, "Self-similarity of complex networks and hidden metric spaces," Phys Rev Lett, vol. 100, p. 078701, 2008.

[25]

M. Boguñá and D. Krioukov, "Navigating ultrasmall worlds in ultrashort time," Phys Rev Lett, vol. 102, p. 058701, 2009.

[26]

M. Gromov, Metric Structures for Riemannian and Non-Riemannian Spaces. Boston: Birkhäuser, 2007.

[27]

D. Burago, Y. Burago, and S. Ivanov, A Course in Metric Geometry. Providence: AMS, 2001.

[28]

J. W. Anderson, Hyperbolic Geometry. London: Springer-Verlag, 2005.

[29]

J. Cannon, W. Floyd, R. Kenyon, and W. Parry, Flavors of Geometry, ch. Hyperbolic Geometry. Berkeley: MSRI, 1997.

[30]

M. R. Bridson and A. Haefliger, Metric Spaces of Non-Positive Curvature. Berlin: Springer-Verlag, 1999.

[31]

P. Mahadevan, D. Krioukov, K. Fall, and A. Vahdat, "Systematic topology analysis and generation using degree correlations," in SIGCOMM, 2006.

[32]

"University of Oregon RouteViews Project." http://www.routeviews.org/.

[33]

"The DIMES project." https://en.wikipedia.org/wiki/DIMES.

[34]

C. Manning, P. Raghavan, and H. Schütze, Introduction to Information Retrieval. Cambridge: Cambridge University Press, 2008.

[35]

X. Dimitropoulos, D. Krioukov, G. Riley, and kc claffy, "Revealing the Autonomous System taxonomy: The machine learning approach," in PAM, 2006.

[36]

L. Gao, "On inferring Autonomous System relationships in the Internet," IEEE ACM T Network, vol. 9, no. 6, 2001.

[37]

L. Subramanian, S. Agarwal, J. Rexford, and R. H. Katz, "Characterizing the Internet hierarchy from multiple vantage points," in INFOCOM, 2002.

[38]

X. Dimitropoulos, D. Krioukov, M. Fomenkov, B. Huffaker, Y. Hyun, kc claffy, and G. Riley, "AS relationships: Inference and validation," Comput Commun Rev, vol. 37, no. 1, 2007.

[39]

D. Michel-Marie and E. Deza, Dictionary of Distances. Amsterdam: Elsevier, 2006.

[40]

A. Clauset, M. E. J. Newman, and C. Moore, "Finding community structure in very large networks," Phys Rev E, vol. 70, p. 066111, 2004.

[41]

L. Danon, J. Duch, A. Arenas, and A. Díaz-Guilera, Large Scale Structure and Dynamics of Complex Networks: From Information Technology to Finance and Natural Science, ch. Community Structure Identification. Singapore: World Scientific, 2007.

[42]

M. Boguñá, R. Pastor-Satorras, A. Díaz-Guilera, and A. Arenas, "Models of social networks based on social distance attachment," Phys Rev E, vol. 70, p. 056122, 2004.

[43]

S. Novikov and I. Taimanov, Modern Geometric Structures and Fields. Providence: AMS, 2006.

[44]

M. Gromov, "Hyperbolic groups," in Essays in Group Theory, vol. 8 of Math Sci Res Inst Publ, pp. 75-263, New York: Springer, 1987.

[45]

"Wikipedia." http://www.wikipedia.org/.

[46]

R. Krauthgamer and J. R. Lee, "Algorithms on negatively curved spaces," in FOCS, 2006.

[47]

I. Abraham, M. Balakrishnan, F. Kuhn, D. Malkhi, V. Ramasubramanian, and K. Talwar, "Reconstructing approximate tree metrics," in PODC, 2007.

[48]

E. Jonckheere, P. Lohsoonthorn, and F. Bonahon, "Scaled Gromov hyperbolic graphs," J. Graph Theory, vol. 57, no. 2, 2008.

[49]

R. Kleinberg, "Geographic routing using hyperbolic space," in INFOCOM, 2007.

[50]

H. Chang, S. Jamin, and W. Willinger, "To peer or not to peer: Modeling the evolution of the Internet's AS-level topology," in INFOCOM, 2006.

[51]

P. Holme, J. Karlin, and S. Forrest, "An integrated model of traffic, geography and economy in the Internet," Comput Commun Rev, vol. 38, no. 3, 2008.

[52]

Digital Envoy, "Netacuity." http://www.digital-element.net/ip_intelligence/ip_intelligence.html.

[53]

A. Okabe, B. Boots, K. Sugihara, and S. N. Chiu, Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. London: Wiley-Interscience, 2000.

[54]

B. Karp and H. T. Kung, "Greedy perimeter stateless routing for wireless networks," in MobiCom, 2000.

[55]

A. Rao, S. Ratnasamy, C. Papadimitriou, S. Shenker, and I. Stoica, "Geographic routing without location information," in MobiCom, 2003.

[56]

R. Gummadi, R. Govindan, N. Kothari, B. Karp, Y.-J. Kim, and S. Shenker, "Reduced state routing in the Internet," in HotNets, 2004.

[57]

Y.-J. Kim, R. Govindan, B. Karp, and S. Shenker, "Geographic routing made practical," in NSDI, 2005.

[58]

F. Kuhn, R. Wattenhofer, and A. Zollinger, "An algorithmic approach to geographic routing in ad hoc and sensor networks," IEEE ACM T Network, vol. 16, no. 1, 2008.

[59]

M. Motiwala, M. Elmore, N. Feamster, and S. Vempala, "Path splicing," in SIGCOMM, 2008.

[60]

C. Gkantsidis, M. Mihail, and A. Saberi, "Conductance and congestion in power law graphs," in SIGMETRICS, 2003.

[61]

O. Cappé, E. Moulines, and T. Rydén, Inference in Hidden Markov Models. New York: Springer, 2007.

[62]

E. Lebhar and N. Schabanel, "Almost optimal decentralized routing in long-range contact networks," in ICALP, 2004.

[63]

G. Manku, M. Naor, and U. Wieder, "Know thy neighbor's neighbor: The power of lookahead in randomized P2P networks," in STOC, 2004.

[64]

C. Martel and V. Nguyen, "Analyzing Kleinberg's (and other) small-world models," in PODC, 2004.

[65]

P. Fraigniaud, C. Gavoille, and C. Paul, "Eclecticism shrinks even small worlds," Distrib Comput, vol. 18, no. 4, pp. 279-291, 2006.

[66]

L. A. Adamic, R. M. Lukose, A. R. Puniyani, and B. A. Huberman, "Search in power-law networks," Phys Rev E, vol. 64, p. 46135, 2001.

[67]

L. A. Adamic and E. Adar, "How to search a social network," Social Networks, vol. 27, no. 3, pp. 187-203, 2005.

[68]

A. Korman and S. Kutten, "Labeling schemes with queries." arXiv:cs.DC/0609163.

[69]

J. M. Guiot, "A modification of Milgram's small world method," Eur J of Soc Psychol, vol. 6, pp. 503-507, 1976.

[70]

A. Dhamdhere and K. Dovrolis, "Ten years in the evolution of the Internet ecosystem," in IMC, 2008.

[71]

CAIDA, "Visualizing Internet topology at a macroscopic scale." https://www.caida.org/projects/as-core/.

[72]

J. Xu and H. Chen, "The topology of dark networks," Commun ACM, vol. 51, no. 10, pp. 58-65, 2008.

[73]

J. Allanach, H. Tu, S. Singh, P. Willett, and K. Pattipati, "Detecting, tracking, and counteracting terrorist networks via hidden Markov models," in IEEE Aerospace Conf, 2004.

[74]

A. Gutfraind, "Understanding terrorist organizations with a dynamical model," Stud Confl Terror, vol. 31, no. 12, 2008.

[75]

D. Monroe, "Just for you," Commun ACM, vol. 52, no. 8, pp. 15-17, 2009.

[76]

G. Uchyigit and M. Y. Ma, Personalization Techniques and Recommender Systems. Singapore: World Scientific, 2008.

[77]

O. Goussevskaia, M. Kuhn, M. Lorenzi, and R. Wattenhofer, "From Web to map: Exploring the world of music," in WI, 2008.

[78]

A. Lakhina, J. Byers, M. Crovella, and P. Xie, "Sampling biases in IP topology measurements," in INFOCOM, 2003.

[79]

D. Achlioptas, A. Clauset, D. Kempe, and C. Moore, "On the bias of traceroute sampling," in STOC, 2005.

[80]

A. Clauset and C. Moore, "Accuracy and scaling phenomena in Internet mapping," Phys Rev Lett, vol. 94, p. 018701, 2005.

[81]

L. Dall'Asta, I. Alvarez-Hamelin, A. Barrat, A. Vázquez, and A. Vespignani, "Exploring networks with traceroute-like probes: Theory and simulations," Theor Comput Sci, Complex Networks, vol. 355, no. 1, pp. 6-24, 2006.

[82]

N. D. Martinez, B. A. Hawkins, H. A. Dawah, and B. P. Feifarek, "Effects of sampling effort on characterization of food-web structure," Ecology, vol. 80, pp. 1044-1055, 1999.

[83]

J. A. Dunne, R. J. Williams, and N. D. Martinez, "Food-web structure and network theory: The role of connectance and size," Proc Natl Acad Sci USA, vol. 99, pp. 12917-12922, 2002.

[84]

T. Ito, T. Chiba, R. Ozawa, M. Yoshida, M. Hattori, and Y. Sakaki, "A comprehensive two-hybrid analysis to explore the yeast protein interactome," Proc Natl Acad Sci USA, vol. 98, pp. 4569-4574, 2001.

[85]

E. Sprinzak, S. Sattath, and H. Margalit, "How reliable are experimental protein-protein interaction data?," J Mol Biol, vol. 327, pp. 919-923, 2003.

[86]

A. Szilágyi, V. Grimm, A. K. Arakaki, and J. Skolnick, "Prediction of physical protein-protein interactions," Phys Biol, vol. 2, pp. S1-S16, 2005.

[87]

J. S. Gutkind (Edt.), Signaling Networks and Cell Cycle Control: The Molecular Basis of Cancer and Other Diseases (Cancer Drug Discovery and Development). New York: Humana Press, 2000.

[88]

B. Groner (Edt.), Targeted Interference with Signal Transduction Events (Recent Results in Cancer Research). Berlin: Springer-Verlag, 2007.

[89]

G. Finocchiaro, F. M. Mancuso, D. Cittaro, and H. Muller, "Graph-based identification of cancer signaling pathways from published gene expression signatures using PubLiME," Nucleic Acids Res, vol. 35, no. 7, pp. 2343-2355, 2007.

[90]

P. Dayan and L. F. Abbott, Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Boston: The MIT Press, 2005.

[91]

J. G. Nicholls, A. R. Martin, B. G. Wallace, and P. A. Fuchs, From Neuron to Brain: A Cellular and Molecular Approach to the Function of the Nervous System. Boston: Sinauer Associates, 2001.

[92]

C. E. Osgood, "Exploration in semantic space: A personal diary," J Soc Issues, vol. 27, pp. 5-64, 1971.

[93]

K. Lund and C. Burgess, "Producing high-dimensional semantic spaces from lexical co-occurrence," Behav Res Meth Ins C, vol. 28, pp. 203-208, 1996.

[94]

T. K. Landauer and S. T. Dumais, "A solution to Plato's problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge," Psychol Rev, vol. 104, pp. 211-240, 1997.

[95]

M. N. Jones and D. J. K. Mewhort, "Representing word meaning and order information in a composite holographic lexicon," Psychol Rev, vol. 114, no. 1, pp. 1-37, 2007.

[96]

B. T. Johns and M. N. Jones, "Predicting word-naming and lexical decision times from a semantic space model," in CogSci, 2008.

[97]

SFI and CAIDA, "Workshop on Networks and Navigation," 2008. https://www.caida.org/workshops/sfi/0808/.

[98]

F. Rao and A. Caflisch, "The protein folding network," J Mol Biol, vol. 342, pp. 299-306, 2004.

[99]

E. Ravasz, S. Gnanakaran, and Z. Toroczkai, "Network structure of protein folding pathways," 2007. arXiv:0705.0912.

[100]

R. Broglia, L. Serrano, and G. Tiana (Edts.), Protein Folding and Drug Design. Amsterdam: IOS Press, 2007.

[101]

M. Franceschetti and R. Meester, Random Networks for Communication: From Statistical Physics to Information Systems. Cambridge: Cambridge University Press, 2008.

[102]

E. M. Daly and M. Haahr, "Social network analysis for routing in disconnected delay-tolerant MANETs," in MobiHoc, 2007.

[103]

A. Miklas, K. Gollu, K. Chan, S. Saroiu, K. Gummadi, and E. de Lara, "Exploiting social interactions in mobile systems," in UbiComp, 2007.

[104]

P. Hui, J. Crowcroft, and E. Yoneki, "BUBBLE rap: Social-based forwarding in delay tolerant networks," in MobiHoc, 2008.

[105]

A. Mtibaa, A. Chaintreau, J. LeBrun, E. Oliver, A.-K. Pietilainen, and C. Diot, "Are you moved by your social network application?," in WOSN, 2008.

[106]

A. Chaintreau, P. Fraigniaud, and E. Lebhar, "Opportunistic spatial gossip over mobile social networks," in WOSN, 2008.

[107]

M. Castells, The Rise of the Network Society (The Information Age: Economy, Society and Culture). Oxford: Blackwell Publishing, 2000.

[108]

https://catalog.caida.org/presentation/2008_krioukov_euvarious.

[109]

CAIDA, "Workshop on the Internet Topology," 2006. https://www.caida.org/workshops/isma/0605/.

[110]

American Physical Society, "Outstanding referees." http://publish.aps.org/OutstandingReferees.

---

Footnotes:

¹We use the term complex network topology to denote topologies with two basic structural properties: strong clustering, i.e., large numbers of 3-cycles, and heavy-tailed distributions of node degrees, i.e., distributions with diverging second moments, which sometimes approximately follow power laws [4]. Notably, wireless networks do not have these properties, see Section 4.

---

File translated from T_{EX by T T H, version 3.72.
On 13 Apr 2010, 11:35.}